
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

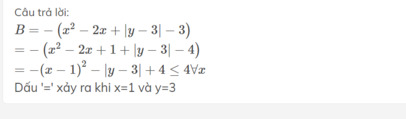


A=3-x2+2x-|y−3|
A=4-(x2-2x+1)-|y-3|
A=4-(x-1)2-|y-3|
Vì \(-\left(x-1\right)^2\le0;-\left|y-3\right|\le0\)
Suy ra:\(4-\left(x-1\right)^2- \left|y-3\right|\le4\)
Dấu = xảy ra khi x-1=0;x=1
y-3=0;y=3
Vậy Max A=4 khi x=1;3

\(A=3-x^2+2x-\left|y-3\right|=-\left(x^2-2x+1\right)+4-\left|y-3\right|=-\left[\left(x-1\right)^2+4-\left|y-3\right|\right]\)
Mà : \(\begin{cases}\left(x-1\right)^2\ge0\\\left|y-3\right|\ge0\end{cases}\)
\(\Rightarrow\left(x-1\right)^2+\left|y-3\right|\ge0\\ \Rightarrow-\left[\left(x-1\right)^2+\left|y-3\right|\right]\le0\\ \Rightarrow A\le4\)
Dấu "=" xảy ra khi x=1;y=3
Vậy MAx A có GTLN khi x=1;y=3


\(B=-\left(x^2-2x+\left|y-3\right|-3\right)\)
\(=-\left(x^2-2x+1+\left|y-3\right|-4\right)\)
\(=-\left(x-1\right)^2-\left|y-3\right|+4\le4\forall x\)
Dấu '=' xảy ra khi x=1 và y=3

a/ A = x2 + (y - 1)4 - 3
Do x2\(\ge\) 0 và (y - 1)4\(\ge\)0
=> A = x2 + (y - 1)4 - 3 \(\ge\)-3
Đẳng thức xảy ra khi: x = 0 và y - 1 = 0 => x = 0 và y = 1
Vậy GTNN của A là -3 khi x = 0 và y = 1
b/ B = 3(x2 - 7) + 2016 = 3x2 - 21 + 2016 = 3x2 + 1995
Mà: 3x2\(\ge\)0 => B = 3x2 + 1995 \(\ge\)1995
Đẳng thức xảy ra khi: 3x2 = 0 => x = 0
Vậy GTNN của B là 1995 khi x = 0
c/ C = (2x + 3)(x - 5) - x(x - 7) = 2x2 - 10x + 3x -15 - (x2 - 7x) = 2x2 - 7x -15 - x2 + 7x = (2x2 -x2) + (-7x + 7x) - 15 = x2 -15
Mà: x2\(\ge\)0 => x2 - 15\(\ge\)-15
Đẳng thức xảy ra khi: x2 = 0 => x = 0
Vậy GTNN cảu C là -15 khi x = 0

