Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Phương trình tọa độ: * Bi A: x 1 = 0 , 1 t 2 (m).
* Bi B: x 2 = 1 − t + 0 , 1 t 2 (m).
b) Khi lăn đến B, tọa độ của bi A là x 1 = 1 m. Ta có: 0 , 1 t 2 = 1 ⇒ t = 10 s.
Nếu coi mặt phẳng nghiêng là đủ dài để bi 2 chuyển động thì quãng đường dài nhất mà 2 bi có thể lăn được cho đến khi dừng v = 0 :
Từ công thức v 2 − v 0 2 = 2 a s ⇒ s m a x = v 2 − v 0 2 2 a = 0 − 1 2 2.0 , 2 = − 2.5 m.
Ta thấy s m a x > A B nên bi 2 có thể lên đỉnh mặt nghiêng.
c) Khi hai hòn bi gặp nhau thì x 1 = x 2 ⇔ 0 , 1 t 2 = 1 − t + 0 , 1 t 2 ⇒ t = 1 s.
Tọa độ gặp nhau: x 1 = x 2 = 0 , 1.1 2 = 0 , 1 m.

Chọn A.
Thời gian lăn hết dốc của hòn bi: \(S=\dfrac{1}{2}at^2\)
\(\Rightarrow t=\sqrt{\dfrac{2S}{a}}=\sqrt{\dfrac{2\cdot15}{3}}=\sqrt{10}s\approx3,2s\)

Từ phép tính trên ta rút ra công thức tính gia tốc của hòn bi là:
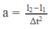
Với I 2 - I 1 = 1 cm ; ∆ t = 0,5 s ; ta có a = 4. 10 - 2 m/ s 2 = 4 cm/ s 2

Giả sử hòn bi chuyển động thẳng nhanh dần đều. Ta hãy tìm quy luật biến đổi của những quãng đường đi được liên tiếp trong những khoảng thời gian bằng nhau.
Đặt I 1 = AB ; I 2 = BC ; I 3 = CD ; I 4 = DE.
Gọi ∆ t là những khoảng thời gian bằng nhan liên tiếp mà hòn bi chuyển động trên các đoạn đường AB, BC, CD và DE.
Giả sử hòn bi xuất phát không vận tốc đầu từ điểm O và sau khoảng thời gian t nó lăn đến điểm A.
Gọi a là gia tốc của hòn bi, ta có OA = 1/2(a t 2 ) (1)
OB = 1/2a t + ∆ t 2 = s + AB (2)
OC = 1/2a t + 2 ∆ t 2 = s + AB + BC (3)
OD = 1/2a t + 3 ∆ t 2 = s + AB + BC + CD (4)
OE = 1/2a t + 4 ∆ t 2 = s + AB + BC + CD + DE (5)
Lần lượt làm các phép trừ vế với vế các phương trình trên, ta có :
(2) - (1): AB = atΔt + 1/2( a ∆ t 2 ) = I 1
(3) - (2): BC = atΔt + 3/2( a ∆ t 2 ) = I 2
(4) - (3): CD = atΔt + 5/2( a ∆ t 2 ) = I 3
(5) - (4): DE = atΔt + 7/2( a ∆ t 2 ) = I 4
Từ các kết quả trên, ta rút ra nhận xét sau :
I 2 – I 1 = a ∆ t 2 ; I 3 – I 2 = a ∆ t 2 ; I 4 – I 3 = = a ∆ t 2
Vậy, trong chuyển động thẳng nhanh dần đều, hiệu những quãng đường đi được trong hai khoảng thời gian liên tiếp bằng nhau là một lượng không đổi.
Áp dụng vào bài toán này (AB = 3 cm, BC = 4 cm, CD = 5 cm và DE = 6 cm) ta thấy :
BC - AB = CD - BC = DE - CD = 1 cm
Vậy, chuyển động của hòn bi là chuyển động thẳng nhanh dần đều.

Tham thảo :
Giải:
a) Gia tốc của vật trên đoạn đường dốc:
s=12at2s=12at2
⇒ a=2st2=2.40102=0,8 (m/s2)a=2st2=2.40102=0,8 (m/s2)
Vận tốc của vật ở chân dốc:
v=√2as=√2.0,8.40=8 (m/s)v=2as=2.0,8.40=8 (m/s)
b) Gia tốc của vật trên đoạn đường ngang:
v′2−v2=2a′s′v′2−v2=2a′s′
⇒ a′=v′2−v22s′=0−822.20=−1,6 (m/s2)a′=v′2−v22s′=0−822.20=−1,6 (m/s2)
c) Thời gian chuyển động trên đoạn đường ngang:
t

a)* Từ đỉnh dốc vận tốc đầu = 0, quả cầu chuyển động nhanh dần
S = 0 + (1/2)at²
=> a = 2S/t² = 2*100/10² = 2 m/s²
*Trên mặt phẳng ngang quả cầu chuyển động chậm dần với gia tốc a', tốc độ đầu v là tốc độ tại chân dốc, tốc độ cuối = 0
v = 0+at = 0 + 2.10 = 20 m/s
Có: 0² - v² = 2.a'S
=> a' = -v²/2S = -20²/2.50 = -4 (m/s²) (dấu - chứng tỏ vật cđộng chậm dần)
b) thời gian chuyển động trên mặt phẳng ngang: t'
0 = v - a't' => t' = v/a' = 20/4 = 5s
thời gian của cả quá trình chuyển động: t + t' = 10 + 5 = 15s
