Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Thời gian lăn hết dốc của hòn bi: \(S=\dfrac{1}{2}at^2\)
\(\Rightarrow t=\sqrt{\dfrac{2S}{a}}=\sqrt{\dfrac{2\cdot15}{3}}=\sqrt{10}s\approx3,2s\)

A là gốc tọa độ, chiều dương từ A-B, gốc thời gian lúc hai vật bắt đầu chuyển động
x1=x0+vo.t+a.t2.0,5=10t-0,1t2
x2=x0+v0.t+a.t2.0,5=560-0,2t2
hai xe gặp nhau x1=x2\(\Rightarrow\)\(\left[{}\begin{matrix}t=40\left(n\right)\\t=-140\left(l\right)\end{matrix}\right.\)
vậy sau 40s hai xe gặp nhau
vị trí hai xe gặp nhau x1=x2=240m

A O x
1) Chọn trục tọa độ Ox như hình vẽ, mốc thời gian lúc ô tô xuất phát.
- Phương trình vận tốc: \(v=v_0+a.t\)
Ban đầu, \(v_0=0\); \(a=0,5m/s^2\)
Suy ra: \(v_1=0,5.t(m/s)\)
- Phương trình tọa độ: \(x=x_0+v_0.t+\dfrac{1}{2}a.t^2\)
\(x_0=0\); \(v_0=0\); \(a=0,5(m/s^2)\)
Suy ra: \(x_1=\dfrac{1}{2}.0,5.t^2=0,25.t^2(m)\)
2) Đổi \(v_{02}=18km/h=5m/s\)
a) Phương trình chuyển động của tàu điện là:
\(x_2=x_0+v_0.t+\dfrac{1}{2}a.t^2=0+5.t+\dfrac{1}{2}.0,3.t^2\)
\(\Rightarrow x_2=5.t+0,15.t^2(m)\)
Ô tôt đuổi kịp tàu điện khi: \(x_1=x_2\)
\(\Rightarrow 0,25.t^2=5.t+0,15.t^2\)
\(\Rightarrow t = 50(s)\)
Vị trí gặp nhau là: \(x=0,25.50^2=625(m)\)
b) Thay \(t=50s\) vào phương trình vận tốc của ô tô và tàu điện ta được:
Vận tốc của ô tô: \(v_1=0,5.t=0,5.50=25(m/s)\)
Vận tốc của tàu điện: \(v_2=5+0,3.t=5+0,3.50=20(m/s)\)


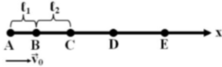
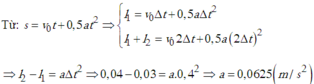
a) Phương trình tọa độ: * Bi A: x 1 = 0 , 1 t 2 (m).
* Bi B: x 2 = 1 − t + 0 , 1 t 2 (m).
b) Khi lăn đến B, tọa độ của bi A là x 1 = 1 m. Ta có: 0 , 1 t 2 = 1 ⇒ t = 10 s.
Nếu coi mặt phẳng nghiêng là đủ dài để bi 2 chuyển động thì quãng đường dài nhất mà 2 bi có thể lăn được cho đến khi dừng v = 0 :
Từ công thức v 2 − v 0 2 = 2 a s ⇒ s m a x = v 2 − v 0 2 2 a = 0 − 1 2 2.0 , 2 = − 2.5 m.
Ta thấy s m a x > A B nên bi 2 có thể lên đỉnh mặt nghiêng.
c) Khi hai hòn bi gặp nhau thì x 1 = x 2 ⇔ 0 , 1 t 2 = 1 − t + 0 , 1 t 2 ⇒ t = 1 s.
Tọa độ gặp nhau: x 1 = x 2 = 0 , 1.1 2 = 0 , 1 m.