K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
15 tháng 11 2015
Với |x - 2009| = 0 có y = +-5 => nghiệm (x, y) = (2009, 5), (2009, -5)
|x - 2009| = 1 không thỏa do 25 - 8 = 17 không chính phương.
Với |x - 2009| ≥ 2 có 8(x - 2009)² ≥ 8*2² = 32 > 25 - y² với mọi y nguyên
HH
0
T
3 tháng 11 2018
\(25-8\left(x-2016^2\right)=\left(y-1\right)^2.\)
\(Nx:\)\(8\left(x-2016\right)^2\ge0;\left(y-1\right)^2\ge0\)
\(\Rightarrow VT=\left(y-1\right)^2\Leftrightarrow8\left(x-2016\right)^2\le25\Rightarrow\left(x-2016\right)^2\le\frac{25}{8}\Rightarrow\left(x-2016\right)^2\le3\)
Mà \(\left(x-2016\right)^2\)là số chính phương \(\Rightarrow\orbr{\begin{cases}\left(x-2016\right)^2=1\\\left(x-2016\right)^2=0\end{cases}}\)
\(\left(x-2016\right)^2=1\Leftrightarrow\orbr{\begin{cases}x-2016=-1\Leftrightarrow x=2015\\x-2016=1\Leftrightarrow x=2017\end{cases}}\)
\(\left(x-2016\right)^2=0\Leftrightarrow x-2016=0\Leftrightarrow x=2016\)
\(Th1\left(x=2015;x=2017\right)\)
\(25-8=\left(y-1\right)^2\Leftrightarrow\left(y-1\right)^2=17\Leftrightarrow y-1=\sqrt{17}\Leftrightarrow y=\sqrt{17}+1\left(loại\right)\)
\(Th2\left(x=2016\right)\)
\(25-0=\left(y-1\right)^2\Leftrightarrow\left(y-1\right)=5\Leftrightarrow y=6\)
Vậy x = 2016 và y = 6
S
2 tháng 11 2018
Ta có: 25-8(x-2016)2=(y-1)2
=>y-1\(\le\)5
Xét TH:
x=2017
=>25-8(2017-2016)2=25-8=17(ko là số chính phương)
TH:x>2017 thì (y-1)2 là số âm
=>x chỉ có thể=2016
=>25-8.0=25=52
=>y-1=5=>y=5+1=6
Từ (1) và (2) suy ra x=2016;y=6
2 tháng 11 2018
\(25-8\left(x-2016\right)^2=\left(y-1\right)^2\)
Ta thấy (y - 1)2 \(\in\) N với mọi y nên 8(x - 2016)2 \(\le\) 25 \(\Leftrightarrow\) (x - 2016)2 < 4. Mà (x - 2016)2 là số chính phương nên (x - 2016)2 = 0 hoặc (x - 2016)2 = 1. Xét 2 trường hợp:
+ TH1: \(\left(x-2016\right)^2=1\Leftrightarrow\orbr{\begin{cases}x=2017\\x=2015\end{cases}}\). Khi đó (y - 1)2 = 24, loại.
+ TH2: \(\left(x-2016\right)^2=0\Leftrightarrow x=2016\). Khi đó (y - 1)2 = 25 \(\Leftrightarrow\orbr{\begin{cases}y=6\\y=-4\end{cases}}\). Loại trường hợp y = -4, ta chọn y = 6.
Vậy x = 2016, y = 6..
AK
29 tháng 3 2018
https://olm.vn/hoi-dap/question/86498.html
- Câu hỏi của Thiều Thị Nhung
LM
2
21 tháng 12 2018
Ta có:
\(25-y^2=8\left(x-100\right)^2\)
Do VP là số chẵn nên VT là số chẵn
Suy ra y2là số lẻ nhỏ hơn hoặc bằng 25
\(\Rightarrow y^2\in\left\{25,16,9,4,1\right\}\)
\(\Rightarrow y\in\left\{5,4,3,2,1\right\}\)
Với y=5=>8(x-100)2=0
=>x=100
Với x=4=>8(x-100)2=9
=>không tồn tại số tự nhiên x
....(như bài mẫu trên)...
Vậy.......
NN
3 tháng 5 2020
1. \(\left(3x-5\right)^{2010}+\left(y-1\right)^{2012}+\left(x-z\right)^{2014}=0\)
Vì \(\left(3x-5\right)^{2010}\ge0\forall x\); \(\left(y-1\right)^{2012}\ge0\forall y\); \(\left(x-z\right)^{2014}\ge0\forall x,z\)
\(\Rightarrow\left(3x-5\right)^{2010}+\left(y-1\right)^{2012}+\left(x-z\right)^{2014}\ge0\)
Dấu " = " xảy ra \(\Leftrightarrow\hept{\begin{cases}3x-5=0\\y-1=0\\x-z=0\end{cases}}\Leftrightarrow\hept{\begin{cases}3x=5\\y=1\\x=z\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{5}{3}\\y=1\\z=\frac{5}{3}\end{cases}}\)
Vậy \(x=z=\frac{5}{3}\)và \(y=1\)
K
28 tháng 12 2018
16: Tìm nghiệm nguyên của phương trình
x2 –xy + y2 = 3
Hướng dẫn:
Ta có x2 –xy + y2 = 3 ⇔ (x- 
)2 = 3 – 
Ta thấy (x- )2 = 3 – ≥ 0
⇒ -2 ≤ y ≤ 2
⇒ y= ± 2; ±1; 0 thay vào phương trình tìm x
Ta được các nghiệm nguyên của phương trình là :
(x, y) = (-1,-2), (1, 2); (-2, -1); (2,1) ;(-1,1) ;(1, -1)
TM
26 tháng 6 2016
2^x= 4^(y-1)
<=> 1^x = 2^(y-1)
<=> 1=2(y-1) Để 2^(y-1) bằng 1 thì 2^(y-1) phải là bậc 0 nên y=1, cho dù x là số nào đi chăng nữa thì đề vẫn thoả mãn
27^y= 3^(x+8)
<=> 9^y = 1^(x+8)
<=> 9^y = 1. Để 9^y bằng 1 thì 9^y phải là bậc 0 nên y=0, còn x là số nào đi nữa thì đề vẫn thoả mãn
Vậy đề này theo mình là tìm y chứ không phải tìm x đâu bạn2^x= 4^(y-1)
<=> 1^x = 2^(y-1)
<=> 1=2(y-1) Để 2^(y-1) bằng 1 thì 2^(y-1) phải là bậc 0 nên y=1, cho dù x là số nào đi chăng nữa thì đề vẫn thoả mãn
27^y= 3^(x+8)
<=> 9^y = 1^(x+8)
<=> 9^y = 1. Để 9^y bằng 1 thì 9^y phải là bậc 0 nên y=0, còn x là số nào đi nữa thì đề vẫn thoả mãn
Vậy đề này theo mình là tìm y chứ không phải tìm x đâu bạn
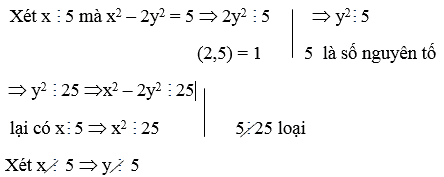
Sửa lại đề:
Tìm x,y thuộc Z biết \(25-y^2=8\left(x-2009\right)^2\)
Ta có:\(\left(x-2009\right)^2\ge0\Rightarrow8\left(x-2009\right)^2\ge0\Rightarrow VP\ge0\Rightarrow VT\ge0\)
Hay \(25-y^2\ge0\)
\(\Rightarrow25-y^2\in\left\{21;25;16;9;0\right\}\)
Đến đây bạn làm từng trường hợp một nhé !