1. Cách viết phương trình đường thẳng đi qua 2 điểm1.1. Cách 1: Giả sử 2 điểm A và B cho trước có tọa độ là: A(a1;a2) và B(b1;b2)Gọi phương trình đường thẳng có dạng d: y=ax+bVì A và B thuộc phương trình đường thẳng d nên ta có hệThay a và b ngược lại phương trình đường thẳng d sẽ được phương trình đường thẳng cần tìm.1.2. Cách 2 giải nhanhTổng quát dạng bài viết phương trình...
Đọc tiếp
1. Cách viết phương trình đường thẳng đi qua 2 điểm
1.1. Cách 1:
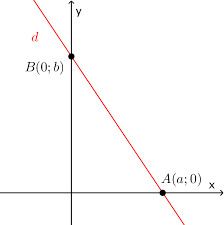
Giả sử 2 điểm A và B cho trước có tọa độ là: A(a1;a2) và B(b1;b2)
- Gọi phương trình đường thẳng có dạng d: y=ax+b
- Vì A và B thuộc phương trình đường thẳng d nên ta có hệ
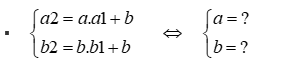
- Thay a và b ngược lại phương trình đường thẳng d sẽ được phương trình đường thẳng cần tìm.
1.2. Cách 2 giải nhanh
Tổng quát dạng bài viết phương trình đường thẳng đi qua 2 điểm: Viết phương trình đường thẳng đi qua 2 điểm A(x1;y1) và B(x2;y2).
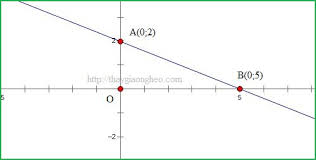
Cách giải:
Giả sử đường thẳng đi qua 2 điểm A(x1;y1) và B(x2;y2) có dạng: y = ax + b (y*)
Vì (y*) đi qua điểm A(x1;y1) nên ta có: y1=ax1 + b (1)
Vì (y*) đi qua điểm B(x2;y2) nên ta có: y2=ax2 + b (2)
Từ (1) và (2) giải hệ ta tìm được a và b. Thay vào sẽ tìm được phương trình đường thẳng cần tìm.
Bài tập ví dụ viết phương trình đường thẳng đi qua 2 điểm
Bài tập 1: Viết phương trình đường thẳng đi qua hai điểm A (1;2) và B(0;1).
Bài giải:
Gọi phương trình đường thẳng là d: y=ax+by=ax+b
Vì đường thẳng d đi qua hai điểm A và B nê n ta có:
⇔ 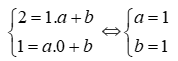
Thay a=1 và b=1 vào phương trình đường thẳng d thì d là: y=x+1
Vậy phương trình đường thẳng đi qua 2 điểm A và B là : y=x+1
Bài tập 2: Cho Parabol (P):y=–ײ . Viết phương trình đường thẳng đi qua hai điểm A và B biết A và B là hai điểm thuộc (P) và có hoành độ lần lượt là 1 và 2.
Bài giải
Với bài toán này chúng ta chưa biết được tọa độ của A và B là như nào. Tuy nhiên bài toán lại cho A và B thuộc (P) và có hoành độ rồi. Chúng ta cần đi tìm tung độ của điểm A và B là xong.
Tìm tọa độ của A và B:
Vì A có hoành độ bằng -1 và thuộc (P) nên ta có tung độ y =−(1)²=–1 => A(1;−1)
Vì B có hoành độ bằng 2 và thuộc (P) nên ta có tung độ y =–(2)²=−4 ⇒ B(2;−4) còn cách khác k ?






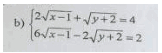


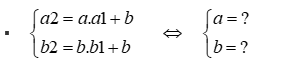

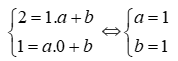


 (Với x > 0; x 1; x4)
(Với x > 0; x 1; x4)
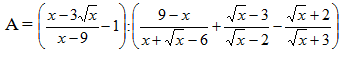

\(3x^2-26x+49=0\left(a=3;b^,=-13;c=49\right)\)
\(\Delta^,=\left(-13\right)^2-3.49=22\Rightarrow\sqrt{\Delta^,}=\sqrt{22}\)
Do \(\Delta^,>0\)nên phương trình đã cho có 2 nghiệm phân biệt là
\(x_1=\frac{13-\sqrt{22}}{3};x_2=\frac{13+\sqrt{22}}{3}\)