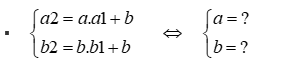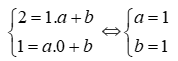Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(3x^2-26x+49=0\left(a=3;b^,=-13;c=49\right)\)
\(\Delta^,=\left(-13\right)^2-3.49=22\Rightarrow\sqrt{\Delta^,}=\sqrt{22}\)
Do \(\Delta^,>0\)nên phương trình đã cho có 2 nghiệm phân biệt là
\(x_1=\frac{13-\sqrt{22}}{3};x_2=\frac{13+\sqrt{22}}{3}\)
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????/
.
.
là hai nghiệm của phương trình. Tìm giá trị của m để: 
. 
a: Gọi phương trình đường thẳng cần tìm là (d): y=ax+b(a<>0)
Vì (d)//y=3x+2 nên \(\left\{{}\begin{matrix}a=3\\b\ne2\end{matrix}\right.\)
Vậy: (d): y=3x+b
Thay x=1 và y=2 vào (d), ta được:
\(b+3\cdot1=2\)
=>b+3=2
=>b=-1
vậy: (d): y=3x-1
b: Gọi phương trình đường thẳng cần tìm là (d): y=ax+b(a<>0)
Vì (d) có tung độ gốc là 3 nên b=3
=>(d): y=ax+3
Thay x=-4 và y=7 vào (d), ta được:
\(-4a+3=7\)
=>-4a=4
=>a=-1
vậy: (d): y=-x+3
c: A(1;4); B(4;8)
=>\(AB=\sqrt{\left(4-1\right)^2+\left(8-4\right)^2}\)
=>\(AB=\sqrt{3^2+4^2}=\sqrt{25}=5\)
c: y=2x-6
=>2x-y-6=0
Khoảng cách từ A(-3;2) đến đường thẳng 2x-y-6=0 là;
\(d\left(A;2x-y-6=0\right)=\dfrac{\left|\left(-3\right)\cdot2+2\left(-1\right)-6\right|}{\sqrt{2^2+\left(-1\right)^2}}\)
\(=\dfrac{\left|-6-2-6\right|}{\sqrt{5}}=\dfrac{14}{\sqrt{5}}\)
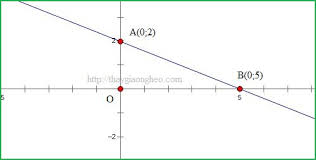
a) Vì A, B thuộc (P) nên:
x A = − 1 ⇒ y A = 1 2 ⋅ - 1 2 = 1 2 x B = 2 ⇒ y B = 1 2 ⋅ 2 2 = 2 ⇒ A − 1 ; 1 2 , B ( 2 ; 2 )
b) Gọi phương trình đường thẳng (d) là y = ax + b.
Ta có hệ phương trình:
− a + b = 1 2 2 a + b = 2 ⇔ 3 a = 3 2 2 a + b = 2 ⇔ a = 1 2 b = 1
Vậy (d): y = 1 2 x + 1 .
c) (d) cắt trục Oy tại điểm C(0; 1) và cắt trục Ox tại điểm D(– 2; 0)
=> OC = 1 và OD = 2
Gọi h là khoảng cách từ O tới (d).
Áp dụng hệ thức về cạnh và đường cao vào ∆ vuông OCD, ta có:
1 h 2 = 1 O C 2 + 1 O D 2 = 1 1 2 + 1 2 2 = 5 4 ⇒ h = 2 5 5
Vậy khoảng cách từ gốc O tới (d) là 2 5 5 .