Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

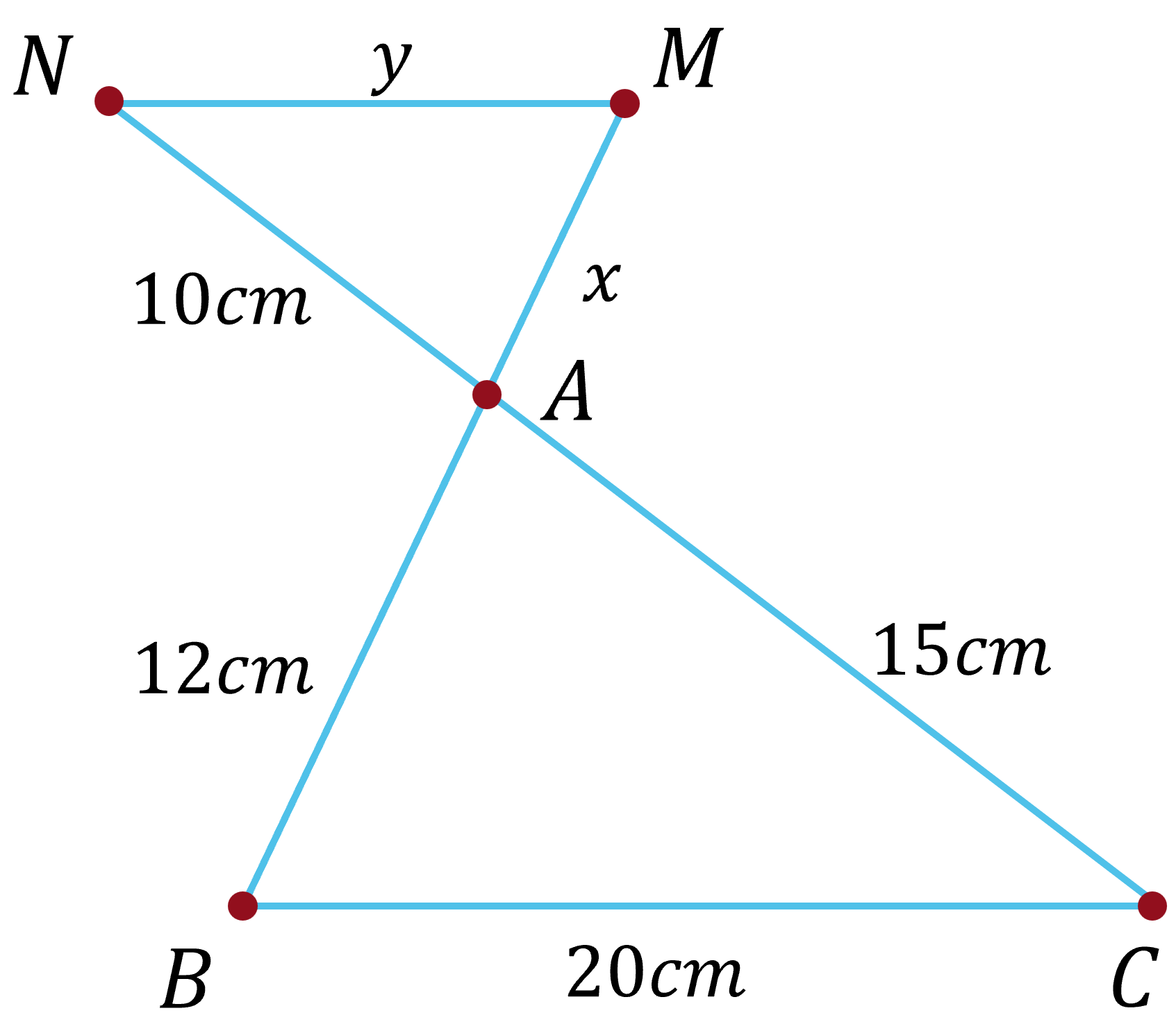
Vì MN // BC theo Talet ta có:
\(\dfrac{y}{20}\) = \(\dfrac{10}{15}\) = \(\dfrac{x}{12}\) => x = \(\dfrac{10}{15}\) . 12 = 8; y = \(\dfrac{10}{15}\) . 20 = \(\dfrac{40}{3}\)

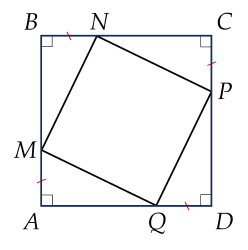
a) Do ABCD là hình vuôn nên:
\(AB=BC=CD=AD\)
Mà: \(\left\{{}\begin{matrix}AB=AM+MB\\BC=BN+NC\\CD=CP+PD\\AD=DQ+QA\end{matrix}\right.\)
Lại có: \(AM=BN=CP=DQ\)
\(\Rightarrow MB=NC=PD=QA\left(dpcm\right)\)
b) Xét \(\Delta QAM\) và \(\Delta NCP\) có:
\(\widehat{A}=\widehat{C}=90^o\left(gt\right)\)
\(AM=CP\left(gt\right)\)
\(QA=NC\left(cmt\right)\)
\(\Rightarrow\Delta QAM=\Delta NCP\left(c.g.c\right)\)
c) Xét các tam giác: \(\Delta QAM,\Delta NCP,\Delta PDQ,\Delta MBN\) ta có:
\(\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=90^o\left(gt\right)\)
\(AM=BN=CP=DQ\left(gt\right)\)
\(MB=NC=PD=QA\left(cmt\right)\)
\(\Rightarrow\Delta QAM=\Delta NCP=\Delta PDQ=\Delta MBN\left(c.g.c\right)\)
\(\Rightarrow MQ=QP=PN=NM\) (các cạnh tương ứng)
\(\Rightarrow MNPQ\) là hình thoi (1)
Xét tam giác QAM ta có:
\(\widehat{QMA}+\widehat{AQM}=180^o-90^o=90^o\)
Mà: \(\Delta QAM=\Delta MBN\left(cmt\right)\)
\(\Rightarrow\widehat{BMN}=\widehat{AQM}\) (hai góc tương ứng)
\(\Rightarrow\widehat{BMN}+\widehat{QMA}=90^o\)
Lại có: \(\widehat{BMN}+\widehat{QMA}+\widehat{NMQ}=180^o\)
\(\Rightarrow\widehat{NMQ}=180^o-90^o=90^o\) (2)
Từ (1) và (2) ta có MNPQ là hình vuông
a) ����ABCD là hình vuông nên ��=��=��=��AB=BC=CD=DA
Mà ��=��=��=��AM=BN=CP=DQ.
Trừ theo vế ta được ��−��=��−��=��−��=��−��AB−AM=BC−BN=CD−CP=DA−DQ
Suy ra ��=��=��=��MB=NC=PD=QA
Xét tam giác QAM và tam giác NPC có:
góc A = góc C = 90 độ
AQ=NC(cmt)
AM=CP(gt)
=>Tam giác QAM= tam giác NPC(c.g.c)
c)=> NP = MQ ( hai cạnh tương ứng)
Chứng minh tương tự như phần b ta có: Tam giác QAM= tam giác PDQ và tam giác QAM= tam giác MBN
Khi đó: MQ=PQ, MN=MQ và góc AMQ= góc DQP
Mà góc AMQ+AQM=90 độ
=>góc DQP+ góc AQM= 90 độ
Do đó góc MQP = 90 độ
tứ giác MNPQ có bốn cạnh bằng nhau nên là hình thoi
Lại có góc MQP = 90 độ nên là hình vuông
Vậy tứ giác MNPQ là hình vuông

Giải:
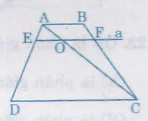
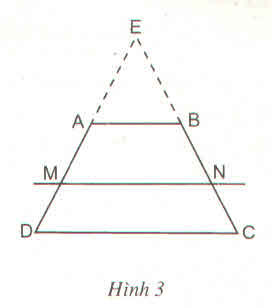
a) Nối AC cắt EF tại O
∆ADC có EO // DC => AEEDAEED = AOOCAOOC (1)
∆ABC có OF // AB => AOOCAOOC = BFFCBFFC (2)
Từ 1 và 2 => AEEDAEED = BFFCBFFC
b) Từ AEEDAEED = BFFCBFFC => AEED+AEAEED+AE= BFFC+BFBFFC+BF
hay AEADAEAD=BFBCBFBC
c) Từ AEEDAEED = BFFCBFFC => AE+EDEDAE+EDED= BF+FCFCBF+FCFC
=> AD