Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khoảng cách giữa 2 vân sáng gần nhau nhất cùng màu với vân trung tâm: \(x_T=k_1i_1=k_2i_2\)(1)
\(\Rightarrow k_1\lambda_1=k_2\lambda_2\Rightarrow\frac{k_1}{k_2}=\frac{\lambda_2}{\lambda_1}=\frac{0,6}{0,48}=\frac{5}{4}\)
\(\Rightarrow\begin{cases}k_1=5\\k_2=4\end{cases}\)
Thay vào (1) \(x_T=5i_1=4i_2\)
Như vậy tại vị trí 2 vân trùng nhau kể từ vân trung tâm có vân bậc 5 của \(\lambda_1\) và bậc 4 của \(\lambda_2\)
Do đó, giữa 2 vân sáng cùng màu vân trung tâm có: 4 vân sáng λ1 và 3 vân sáng λ2.
Đáp án A.

Đáp án D
+ Điều kiện để hai vân tối trùng nhau λ 1 λ 2 = 2 k 2 + 1 2 k 2 + 1 = n 2 n 1 với n1 và n2 là các số lẻ → loại đáp án B và C
Vì tính lặp lại tuần hoàn của các vị trí vân tối trùng nhau, do vậy để đơn giản ta xét hai vân tối trùng nhau gần nhất nằm đối xứng qua vân sáng trung tâm.
+ Theo giả thuyết bài toán, giữa 6 vân tối liên tiếp có 35 vạch sáng, nghĩa là giữa hai vân tối liên tiếp sẽ có 7 vạch sáng.
+ Số vân đơn sắc λ1 nhiều hơn số vân đơn sắc λ2 là 2 vân, vậy giữa hai vân tối có vị trí trùng nhau của hai vân sáng, trường hợp khả dĩ nhất là trùng một vân, khi đó vân trùng là vân trung tâm, và số vân sáng đơn sắc λ1 là 4, số vân sáng đơn sắc λ2 là 2
→ Vị trí trùng nhau của hai vân tối là vân tối bậc 3 của λ1 và vân tối bậc 2 của λ2
Ta có λ 1 λ 2 = 1 , 5 2 , 5 ⇒ λ 2 = 0 , 75 μ m

Số vân sáng quan sát được là
\(N_s = N_{s1}+ N_{s2}-N_{trung nhau} =17.\)
Số vân sáng của \(\lambda_1\) trên trường giao thoa L là
\(N_{s1}= 2.[\frac{L}{2i_1}]+1 = 9.\)
=> \(N_{s2}= N_s-N_{s1}-N_{trung nhau} = 17-9+3=11.\)

1) i=2mm.
Biết bề rộng miền giao thoa L=3cm=30mm, ta có:
\(\frac{L}{2i}=7,5\) Phần nguyên n=7.
Suy ra số vân sáng: \(N_1=2n+1=15\) vân;
Số vân tối: \(N_2=2\left(n+1\right)=16\) vân.
2) Khi thực hiện thí nghiệm trong môi trường nước, bước sóng ánh sáng là \(\lambda'=\frac{\lambda}{n}\), do đó khoảng vân bây giờ là : \(I'=\lambda'\frac{D}{a}=\frac{i}{n}=1,5mm\)
Ta có: \(\frac{L}{2i'}=10\). Suy ra số vân sáng:\(N'_1=2n+1=21\) vân
Số vân tối : \(N'_2=2n=20\) vân.

\(i_1 = \frac{\lambda_1D_1}{a}\)
\(i_2 = \frac{\lambda_2D_2}{a}\)
=> \(\frac{i_1}{i_2} = \frac{\lambda_1D_1}{\lambda_2D_2} \)
=> \(\frac{\lambda_1}{\lambda_2} = \frac{i_1D_2}{i_2D_1} = \frac{1.2}{3.1}= \frac{2}{3}\) (do \(i_2 = 3i_1; D_2 = 2D_1\))
=> \(\lambda_2 = \frac{3\lambda_1}{2} = \frac{3.0,4}{2} = 0,6 \mu m.\)
Chọn đáp án.A

Tịnh tiến màn quan sát lại gần mặt phẳng chưa hai khe 25 cm tức là \(D' = D-0,25.\)
\(i_1 = \frac{\lambda D}{a}\\
i_2 =\frac{\lambda (D-0,25)}{a} \)=> \(\frac{i}{i'}= \frac{D}{D-0,25}= \frac{5}{4}\)
=> \(D = 5.0,25 = 1,25m.\)
=> \(\lambda = \frac{i.a}{D}= 0,48 \mu m.\)
Chú ý là giữ nguyên đơn vị i (mm); a (mm) ; D (m) thì đơn vị bước sóng \(\lambda (\mu m)\).

Điều kiện để hai vân tối trùng nhau là
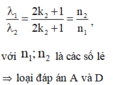
Vì tính lặp lại tuần hoàn của các vị trí vân tối trùng nhau , do vậy để đơn giản ta xét hai vân tối trùng nhau gần nhất nằm dói xứng qua vân sang trung tâm
Theo đề ra thì : giữa 6 vân tối liên tiếp có 35 vạch sang, nghĩa là giữa hai vân tối liên tiếp sẽ có 7 vạch sang
Số vân đơn sắc λ 1 nhiều hơn số vân đơn sắc λ 2 là hai vân . vậy giữa hai vân tối có vị trí trùng nhau của hai vân sang, trường hợp khả dĩ nhất là trùng 1 vân, khi đó vân sang trùng là vân trung tâm, số vân sang đơn sắc v là 4, số vân sang đơn sắc λ 2 là 2
→ Vị trí trùng nhau của hai vân tối là vân tối bậc 3 của λ 2 và vân tối bậc 2 của λ 2
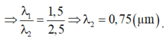
Đáp án C

\( i = \frac{\lambda D}{a}= 0,64 mm.\)
Số vân tối quan sát được trên màn là
\(N_t = 2.[\frac{L}{2i}+0,5]=2.9=18.\)

Tóm tắt:
\(a=10^{-3}m\)
\(D=0,5m\)
\(\lambda_1=0,64\mu m\)
\(\lambda_2=0,6\mu m\)
\(\lambda_3=0,54\mu m\)
\(\lambda_4=0,48\mu m\)
\(\Delta x=?\)
Giải:
Khi vân sáng trùng nhau:
\(k_1\lambda_1=\)\(k_2\lambda_2=\)\(k_3\lambda_3=\)\(k_4\lambda_4\) \(\Leftrightarrow k_10,64\)\(=k_20,6\)\(=\)\(k_30,54\)\(=k_40,48\)
\(\Leftrightarrow\)\(k_164=k_260=k_354=k_448\) \(\Leftrightarrow\) \(k_164=k_260=k_354=k_448\)
\(\Leftrightarrow k_132=k_230=k_327=k_424\)
BSCNN( 32;30;27;24 ) = 4320
\(k_1=\frac{4320}{32}=135\)
\(k_2=\frac{4320}{30}=144\)
\(k_3=\frac{4320}{27}=160\)
\(k_4=\frac{4320}{24}=180\)
Vậy \(\Delta x=135i_1=144i_2=160i_3=180i_4\)\(=0,0432m=4,32cm\)
\(\rightarrow D\)
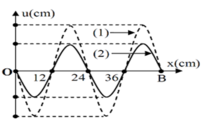
Cách giải:
Gọi N1 là tổng số bạch màu ứng với bước sóng λ 1 và N2 là tổng số vạch màu ừng với bước sóng λ 2 quan sát trên khoảng rộng L.
Trong khoảng L quan sát được 6 vạch tối, hai trong 6 vạch tối nằm ngoài cùng khoảng L, các vạch tối cách đều nhau giữa hai vạch tối có 35/5 = 7 vân sáng ứng với hai bức xạ λ 1 và λ 2
N1 + N2 = 35-5; và N1 – N2 = 10 => N1 = 20; và N2 = 10
Số vân sáng thực ứng với bức xạ λ 1 là 20 + 5 = 25 (tính cả các vân trùng)
Số vân sáng thực ứng với bức xạ λ 2 là 10 + 5 = 15 (tính cả các vân trùng)
Ta có
Đáp án D