

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Chọn C.
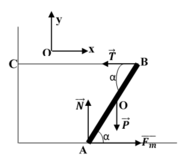
Ta có: P = m.g = 150 N
Theo điều kiện cân bằng của vật rắn quay quanh trục


Chọn C.
Ta có: P = m.g = 150 N
Theo điều kiện cân bằng của vật rắn quay quanh trục A: MT = MP ⟺ T.dT = P.dP

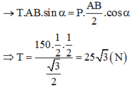
Chọn hệ quy chiếu Oxy như hình vẽ.
Theo điều kiện cân bằng của vật rắn:
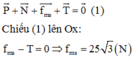

a. Ta có
P = m g = 1 , 5.10 = 150 ( N )
Theo điều kiện cân bằng của vật rắn quay quanh trục A:
M T = M P ⇒ T . d T = P . d P ⇒ T . A B . sin α = P . A B 2 . cos α ( * ) ⇒ T = 150. 1 2 . 1 2 3 2 = 25 3 ( N )

Chọn hệ quy chiếu Oxy như hình vẽ
Theo điều kiện cân bằng của vật rắn
P → + N → + f → m s + T → = 0 →
Chiếu (1) lên Ox
f m s − T = 0 ⇒ f m s = 25 3 ( N )
Chiếu (1) lên Oy
P − N = 0 ⇒ N = P = 150 ( N )
b. Từ ( * ) ta có T = P . cotg α 2
Lúc này F → m s là lực ma sát nghỉ
⇒ F m s ≤ k N ⇒ 1 2 m g . cot g α ≤ k . m g ⇒ cot g α ≤ 2 k = 3 ⇒ α ≥ 30 0

45 P N F dh
Chọn trục toạ độ như hình vẽ.
Vật ở VTCB lò xo bị nén \(\Delta \ell_0\)
Vật đang đứng yên ở VTCB, hợp lực tác dụng lên vật bằng 0
\(\Rightarrow \vec{P}+\vec{F_{dh}}+\vec{N}=\vec{0}\)
Chiếu lên trục toạ độ ta được: \(P.\sin 45^0-F_{dh}=0\)
\(\Rightarrow mg.\sin 45^0=k.\Delta \ell_0\)
\(\Rightarrow k=\dfrac{mg.\sin 45^0}{\Delta \ell_0}=\dfrac{0,2.10.\sin 45^0}{0,02}=50\sqrt 2(N/m)\)
Chọn C.

Ta có :
Trọng lực của thanh đặt ở trung điểm thanh (gọi G là trung điểm thanh AB)
Ta giải bài toán trong trường hợp tổng,
Áp dụng quy tắc momen trục quay tại B:
\(mg.BGsin\alpha=F.BA\)
\(\rightarrow F=mg\frac{BGsin\alpha}{BA}=50.10\frac{sin\alpha}{2}=250sin\alpha\)
Phản lực của tường phải cân bằng với F và P.
Phản lực theo phương ngang: \(N_x=F.sin\alpha\)
Phản lực theo phương thẳng đứng:\(N_y=mg-F.cos\alpha\)
Gọi góc hợp giữa phản lực và phương ngang là \(\phi\)
\(tan\phi=\frac{Ny}{Nx}=\frac{mg-Fcos\alpha}{Fsin\alpha}\)
\(=\frac{500-250sin\alpha.cosalpha}{250sinalpha^2}=\frac{2-sin\alpha.cosalpha}{sinalpha^2}\)
Độ lớn của phản lực:
\(N=\sqrt{N_x^2+N^2_y}=\sqrt{F^2+m^2g^2-2mgFcosalpha}\)
Trong 2 trường hợp góc α này chúng ta thay số và tìm các giá trị cần tìm