K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
9 tháng 3 2020
a, Đặt \(x^2-4x+8=a\left(a>0\right)\)
\(\Rightarrow a-2=\frac{21}{a+2}\)
\(\Leftrightarrow a^2-4=21\Rightarrow a^2=25\Rightarrow a=5\)
Thay vào là ra
9 tháng 3 2020
b) ĐK: \(y\ne1\)
bpt <=> \(\frac{4\left(1-y\right)}{1-y^3}+\frac{1+y+y^2}{1-y^3}+\frac{2y^2-5}{1-y^3}\le0\)
<=> \(\frac{3y^2-3y}{1-y^3}\le0\)
\(\Leftrightarrow\frac{y\left(y-1\right)}{\left(y-1\right)\left(y^2+y+1\right)}\ge0\)
\(\Leftrightarrow\frac{y}{y^2+y+1}\ge0\)
vì \(y^2+y+1=\left(y+\frac{1}{2}\right)^2+\frac{3}{4}>0\)
nên bpt <=> \(y\ge0\)
29 tháng 12 2015
Bạn đăng từng câu một thì sẽ có người giúp bạn đấy!
Tick cho mình nhé!
TT
1
NQ
3
9 tháng 5 2018
a) \(\sqrt{x^2+4x+5}=1\)
\(\Leftrightarrow\sqrt{x^2+4x+5}=\sqrt{1}\)
\(\Rightarrow x^2+4x+5=1\)
\(\Rightarrow x^2+4x+4=0\)
\(\Rightarrow\left(x+2\right)^2=0\)
\(\Rightarrow x+2=0\)
\(\Rightarrow x=-2\)
b) \(\sqrt{x^2+4x+4}=2x-1\)
\(\Leftrightarrow\left(\sqrt{x^2+4x+4}\right)^2=\left(2x-1\right)^2\)
\(\Leftrightarrow x^2+4x+4=\left(2x-1\right)^2\)
\(\Leftrightarrow\left(x+2\right)^2=\left(2x-1\right)^2\)
\(\Rightarrow x+2=2x-1\)
\(\Rightarrow-x=-3\)
\(\Rightarrow x=3\)
10 tháng 5 2018
\(\sqrt{x^2+4x+5}=1\Leftrightarrow x^2+4x+5=1\Leftrightarrow x^2+4x+4=0\Leftrightarrow x=-2\)
26 tháng 1 2021
a)(x2-2x+1)-4=0
⇔(x-1)2-4=0
⇔(x-1-2)(x-1+2)=0
⇔(x-3)(x+1)=0
⇔x-3=0 hoặc x+1=0
1.x-3=0⇔x=3
2.x+1=0⇔x=-1
vậy phương trình có 2 nghiệm:x=3 và x=-1
DP
2
S
21 tháng 3 2020
\(\frac{5}{x^2+3x-2x-6}-\frac{2}{x^2+x+3x+3}=\frac{-3}{2x-1}\Leftrightarrow\frac{5}{\left(x+3\right)\left(x-2\right)}-\frac{2}{\left(x+3\right)\left(x+1\right)}=\frac{-3}{2x-1}\)
\(\Leftrightarrow\frac{5\left(x+1\right)-2\left(x-2\right)}{\left(x+1\right)\left(x+2\right)\left(x-2\right)}=\frac{3x+9}{\left(x+1\right)\left(x+2\right)\left(x-2\right)}=\frac{-3}{2x-1}\Leftrightarrow\frac{-x-9}{\left(x+1\right)\left(x+2\right)\left(x-2\right)}=\frac{1}{2x-1}\)
\(\Leftrightarrow\left(1-2x\right)\left(x+9\right)=\left(x+1\right)\left(x+2\right)\left(x-2\right)\)
HV
2
19 tháng 4 2020
\(\frac{4x-5}{x-1}=2+\frac{x}{x-1}\)
\(\Leftrightarrow\frac{4x-5}{x-1}=\frac{2\left(x-1\right)}{x-1}+\frac{x}{x-1}\)
\(\Leftrightarrow4x-5=2x-2+x\)
\(\Leftrightarrow4x-2x-x=-2+5\)
\(\Leftrightarrow x=3\)
Vậy phuong trình có tập nghiệm là S = { 3 }
19 tháng 4 2020
\(\frac{4x-5}{x-1}=2+\frac{x}{x-1}ĐKXĐ:x\ne1\)
\(\frac{4x-5}{x-1}=\frac{2\left(x-1\right)}{x-1}+\frac{x}{x-1}\)
\(4x-5=2x-2+x\)
\(4x-5-2x+2-x=0\)
\(x-3=0\)
\(x=3\)Theo ĐKXĐ => tm
6 tháng 4 2020
1/ \(3x^2-2x=0\Leftrightarrow x\left(3x-2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\frac{2}{3}\end{matrix}\right.\)
Vậy .....................
2/ \(4x^2-4x+\frac{1}{2}=0\)
\(\Delta=b'^2-ac=2^2-\frac{4.1}{2}=2\)
\(\Rightarrow\left[{}\begin{matrix}x_1=\frac{2+\sqrt{2}}{4}\\x_2=\frac{2-\sqrt{2}}{4}\end{matrix}\right.\)
Vậy ........................
3/ \(\left(x-1\right)\left(x^2+5x-2\right)-\left(x^3-1\right)=0\)
<=> \(\left(x-1\right)\left(x^2+5x-2\right)-\left(x-1\right)\left(x^2+x+1\right)=0\)
<=> \(\left(x-1\right)\left(4x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\frac{3}{4}\end{matrix}\right.\)
Vậy ......................
6 tháng 4 2020
a) Ta có: \(3x^2+2x=0\)
\(\Leftrightarrow x\left(3x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\3x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\3x=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\frac{-2}{3}\end{matrix}\right.\)
Vậy: \(x\in\left\{0;\frac{-2}{3}\right\}\)
b) Ta có: \(4x^2-4x+\frac{1}{2}=0\)
\(\Leftrightarrow4x^2-4x+1-\frac{1}{2}=0\)
\(\Leftrightarrow\left(2x-1\right)^2-\frac{1}{2}=0\)
\(\Leftrightarrow\left(2x-1\right)^2=\frac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=\sqrt{\frac{1}{2}}\\2x-1=-\sqrt{\frac{1}{2}}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=\sqrt{\frac{1}{2}}+1\\2x=-\sqrt{\frac{1}{2}}+1\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{2+\sqrt{2}}{4}\\x=\frac{2-\sqrt{2}}{4}\end{matrix}\right.\)
Vậy: \(x=\frac{2\pm\sqrt{2}}{4}\)
AM
1
DH
11 tháng 8 2017
câu 1 theo cách nhẩm nghiệm thì mình thấy hình như bn chép sai đề r
x2-1/x-1>0=>(x-1)(x+1)/x-1>0 rút gọn vế trái còn x+1>0=.x>-1
x2-6x+9>0=>x-3(x-3)>0=>xảy ra khi 2 thừa số này cùng dấu =>x>3 hoặc x<3
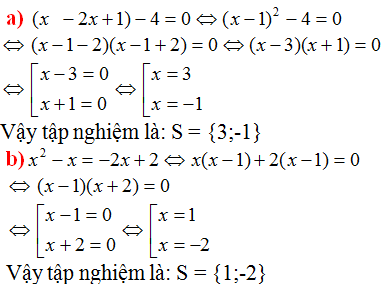
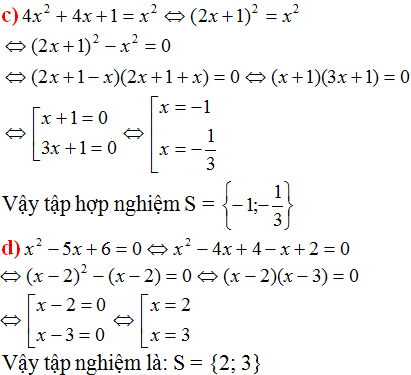
4x2 + 4x + 1 = x2
⇔ 4x2 + 4x + 1 – x2 = 0
⇔ (4x2 + 4x + 1) – x2 = 0
⇔ (2x + 1)2 – x2 = 0
⇔ (2x + 1 – x)(2x + 1 + x) = 0
(Sử dụng hằng đẳng thức)
⇔ (x + 1)(3x + 1) = 0
⇔ x + 1 = 0 hoặc 3x + 1 = 0
+ x + 1 = 0 ⇔ x = -1.
+ 3x + 1 = 0 ⇔ 3x = -1 ⇔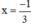
Vậy phương trình có tập nghiệm