Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Txđ: D =\(\left[1998;+\infty\right]\)
b) \(f\left(2002\right)=620000\) con.
\(g\left(1999\right)=380000\) con.
\(h\left(2000\right)=100000\) con.
c) \(h\left(1999\right)=30000\) con; \(h\left(2002\right)=210000\).
\(h\left(2002\right)-h\left(1999\right)=210000-30000=180000\).
Ý nghĩa: Hiệu \(h\left(2002\right)-h\left(1999\right)\) thể hiện sự tăng trưởng sản lượng ngan qua giai đoạn 1999 - 2002.

1: ĐKXĐ: \(x^3-6x^2+11x-6< >0\)
\(\Leftrightarrow x^3-x^2-5x^2+5x+6x-6\ne0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2-5x+6\right)\ne0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)\left(x-3\right)\ne0\)
hay \(x\notin\left\{1;2;3\right\}\)
2; ĐKXĐ: \(\left\{{}\begin{matrix}3-2x>=0\\x+1< >-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< =\dfrac{3}{2}\\x< >-2\end{matrix}\right.\)
3: ĐKXĐ: \(\left\{{}\begin{matrix}x+2< >0\\x-1< >0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< >-2\\x< >1\end{matrix}\right.\Leftrightarrow x\in R\)

What? Lớp 10? Mí bài nỳ dễ mak! Trên lp cs hc mak k giải đc thì thui lun!![]()

a) Tập xác định của f(x) :
A = {x ∈ R | x2 + 3x + 4 ≥ 0 và -x2 + 8x – 15 ≥ 0}
- x2 + 3x + 4 có biệt thức Δ = 32 – 16 < 0
Theo định lí dấu của tam thức:
x2 + 3x + 4 ≥ 0 ∀x ∈R
-x2 + 8x – 15 = 0 ⇔ x1 = 3, x2 = 5
-x2 + 8x – 15 > 0 ⇔ 3 ≤ x ≤ 5 ⇒ A = [3, 5]
b) A/B = [3, 4]
R\(A\B) = (-∞, 3) ∪ (4, +∞)

a, x2 - 2x + 1 + x2 + 6x + 9 = 32
<=. 2x2 + 4x - 22 = 0
<=> x2 + 2x - 11 = 0
\(\Delta' = 1+11=12 \)
PT có 2 nghiệm
x = -1 \(\pm \) 2\(\sqrt{3}\)

\(A=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=\sqrt{\left(-\dfrac{5}{\sqrt{3}}\right)^2-4\cdot\dfrac{-\sqrt{2}}{\sqrt{3}}}=\sqrt{\dfrac{25+4\sqrt{6}}{3}}\)
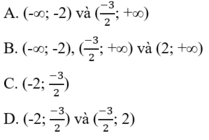



Cách 1. Lập bảng xét dấu.
Cách 2. f(x) không xác định khi x = 2 và 2 ∈ ((-3)/2; +∞) nên A sai. Dễ thấy x = (-7)/4 thì x 2 – 4 < 0; x – 2 < 0; 2x + 3 < 0 ⇒ f(x) < 0, vì vậy C và D sai.
Đáp án: B