Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

f(2002) = 620000 (con)
g(1999) = 380000 (con)
h(2000) = 100000 (con)
Năm 2002 sản lượng của trang trại là 620 000 con vịt ; năm 1999 sản lượng là 380 000 con gà ; năm 2000 trang trại có sản lượng là 100 000 con ngan lai.

h(2002) - h(1999) = 210000 - 30000 = 180000 (con)
Sản lượng ngan lai của trang trại năm 2002 tăng 180 000 con so với năm 1999.

Tập xác định của cả ba hàm số y = f(x), y = g(x) và y = h(x) là:
D = {1998, 1999, 2000, 2001, 2002}

a) f(x) = (x+2)(x-1)
f(x) > 0 với x < -2 hoặc x > 1
f(x) ≤ 0 với -2 ≤ x ≤ 1
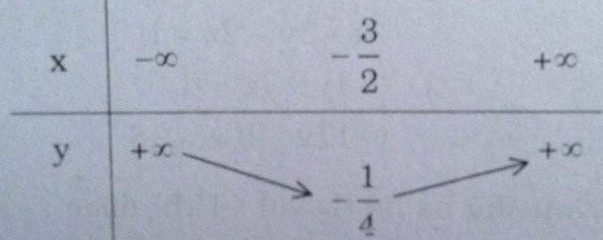
b) y = 2x (x + 2) = 2(x+1)2 – 2
Bảng biến thiên:
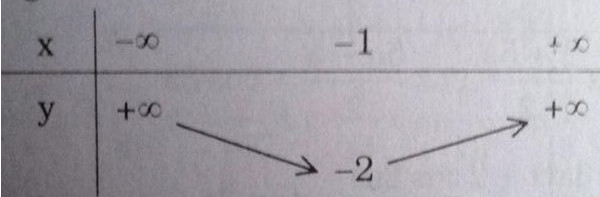
Hàm số : y = \(\left(x+2\right)\left(x+1\right)=\left(x+\dfrac{3}{2}\right)^2-\dfrac{1}{4}\)
Bảng biến thiên :
Đồ thị (C1) và (C2)
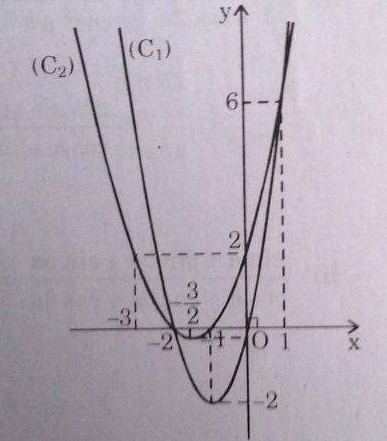
Hoành độ các giao điểm A và B của (C1) và (C2) là nghiệm của phương trình f(x) = 0 ⇔ x1 = -2, x2 = 1
⇔ A(-2, 0) , B(1, 6)
c) Giải hệ phương trình
\(\left\{{}\begin{matrix}\dfrac{ac-b^2}{4a}\\a\left(-2\right)^2+b\left(-2\right)+c=0\\a\left(1\right)^2+b\left(1\right)+c=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2,b=0,c=8\\a=-\dfrac{2}{9},b=\dfrac{16}{9},c=\dfrac{40}{9}\end{matrix}\right.\)

a)
f(x) giao trục tại hai Điểm có hoành độ x1=-4; x2=-2
g(x) giao trục hoành duy nhất một điểm hoành độ x=m/2

b) f(x) >g(x) => điểm m/2 phải trong khoảng (-4,-2)
\(-4< \dfrac{m}{2}< -2\Leftrightarrow-8< m< -4\)

a) Với \(x\in\left[0;1\right]\) => x - 2 < 0 => |x - 2| = - (x -2)
Khi đó, \(f\left(x\right)=2\left(m-1\right)x+\frac{m\left(x-2\right)}{-\left(x-2\right)}=2\left(m-1\right)x-m\)
Để f(x) < 0 với mọi \(x\in\left[0;1\right]\) <=> \(2\left(m-1\right)x-m<0\) (*) với mọi \(x\in\left[0;1\right]\)
+) Xét m - 1 > 0 <=> m > 1
(*) <=> \(x<\frac{m}{2\left(m-1\right)}\). Để (*) đúng với mọi \(x\in\left[0;1\right]\) <=> \(\frac{m}{2\left(m-1\right)}\ge1\) <=> 2(m -1) \(\le\)m <=> m \(\le\) 2 <=> m \(\le\) 2
Kết hợp điều kiện m > 1 =>1 < m \(\le\) 2
+) Xét m = 1 thì (*) <=> -1 < 0 luôn đúng => m =1 thỏa mãn
+) Xét m - 1 < 0 <=> m < 1
(*) <=> \(x>\frac{m}{2\left(m-1\right)}\). Để (*) đúng với mọi \(x\in\left[0;1\right]\) <=> \(\frac{m}{2\left(m-1\right)}\le0\) <=> m \(\ge\) 0 (do m< 1 ). Kết hợp m < 1 => 0 \(\le\) m < 1
Kết hợp các trường hợp : Với 0 \(\le\)m \(\le\) 2 thì .....
b) Hoành độ giao điểm của đò thị hàm số với Ox là nghiệm của Phương trình : \(2\left(m-1\right)x+\frac{m\left(x-2\right)}{\left|x-2\right|}=0\) (1)
Đồ thị hàm số cắt Ox tại điểm có hoành độ xo thuộc (1;2) => xo < 2 => |xo - 2| = - (xo - 2)
xo là nghiệm của (1) <=> \(2\left(m-1\right)x_o+\frac{m\left(x_o-2\right)}{\left|x_o-2\right|}=0\) <=> \(2\left(m-1\right)x_o-m=0\)
+) Xét m \(\ne\) 1 thì (2)<=> \(x_o=\frac{m}{2\left(m-1\right)}\). Vì 1 < xo < 2 nên \(1<\frac{m}{2\left(m-1\right)}<2\) <=> \(\begin{cases}\frac{m}{2\left(m-1\right)}-1>0\\\frac{m}{2\left(m-1\right)}-2<0\end{cases}\) <=> \(\begin{cases}\frac{-m+2}{2\left(m-1\right)}>0\left(a\right)\\\frac{-3m+4}{2\left(m-1\right)}<0\left(b\right)\end{cases}\)
Giải (a) <=> 1 < m < 2
Giải (b) <=> m < 1 hoặc m > 4/3
Kết hợp nghiệm của (a) và (b) => 4/3 < m < 2
+) Xét m = 1 thì (2) <=> -1 = 0 Vô lí
Vậy Với 4/3 < m < 2 thì đồ thị hàm số cắt Ox tại điểm thuộc (1;2)

đồ thị hai hàm parabol có một điểm chung khi chúng có chung đỉnh
hay đỉnh I(1,3) của f(x) cũng là đỉnh của g(x)
dẫn đến giá trị nhỏ nhất của hai hàm là bằng nhau.
thế nên bài này sai ngay từ đề bài rồi nhé
hay nói cách khác , không tồn tại hai số a b thỏa mãn điều kiện trên

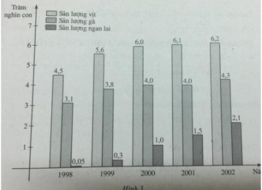
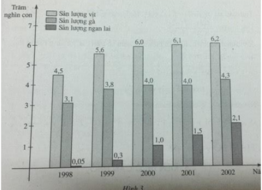
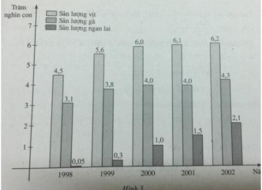


a) Txđ: D =\(\left[1998;+\infty\right]\)
b) \(f\left(2002\right)=620000\) con.
\(g\left(1999\right)=380000\) con.
\(h\left(2000\right)=100000\) con.
c) \(h\left(1999\right)=30000\) con; \(h\left(2002\right)=210000\).
\(h\left(2002\right)-h\left(1999\right)=210000-30000=180000\).
Ý nghĩa: Hiệu \(h\left(2002\right)-h\left(1999\right)\) thể hiện sự tăng trưởng sản lượng ngan qua giai đoạn 1999 - 2002.