
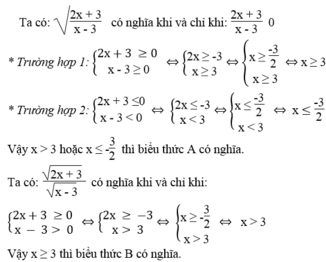
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

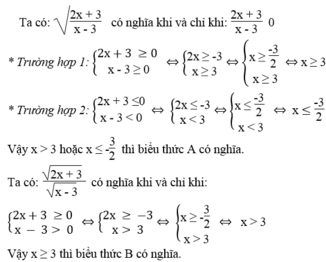

Bài 1:
a) Để A,B có nghĩa \(\Leftrightarrow\begin{cases}2x+3\ge0\\x-3>0\end{cases}\)\(\Leftrightarrow\begin{cases}x\ge-\frac{3}{2}\\x>3\end{cases}\)\(\Leftrightarrow x>3\)
b) Để A= B
\(\Leftrightarrow\sqrt{\frac{2x+3}{x-3}}=\frac{\sqrt{2x+3}}{\sqrt{x-3}}\)
\(\Leftrightarrow\sqrt{\frac{2x+3}{x-3}}-\sqrt{\frac{2x+3}{x-3}}=0\)
\(\Leftrightarrow0x=0\) (thỏa mãn với mọi x>3)
Vậy x>3 thì A=B
a, ĐKXĐ A: \(\frac{2x+3}{x-3}\)\(\frac{2x+3}{x-3}\ge0\Rightarrow\left[\begin{array}{nghiempt}\hept{\begin{cases}2x+3\ge0\\x-3>0\end{array}\right.\\\hept{\begin{cases}2x-3\le0\\x-3< 0\end{array}\right.\end{cases}\Rightarrow\left[\begin{array}{nghiempt}\hept{\begin{cases}x\ge-\frac{3}{2}\\x>3\end{array}\right.\\\hept{\begin{cases}x\le-\frac{3}{2}\\x< 3\end{array}\right.\end{cases}\Rightarrow}\left[\begin{array}{nghiempt}x>-\frac{3}{2}\\x< 3\end{array}\right.}\)
ĐKXĐ B: \(\begin{cases}2x+3\ge0\\x-3>0\end{cases}\Rightarrow\begin{cases}x\ge-\frac{3}{3}\\x>3\end{cases}}\)

a) A có nghĩa khi (2x+3)/(x-3)>= 0
Trường hợp 1:
2x+3>=0
x>= -3/2(1)
×-3>0
x>3(2)
Từ (1),(2)suy ra x>3
●trường hợp 2
2x+3<= 0
x<=-3/2(3)
x-3<0
x<3(4)
Từ (3),(4) suy ra x<=-3/2
Vậy khi x<=-3/2 hoặc x>3 thì A có nghĩa
B có nghĩa khi (2x+3)/(x_3)>=0
•TH1:
2x+3>=0
x>= -3/2(5)
x-3>0
x>3(6)
Từ (5),(6) suy ra x>3
•TH2:
2x+3<=0
x<=-3/2
Vậy khi x<=-3/2 hoặc x>3 thì B có nghĩa
b) A=B khi x<= -3/2 và x>3

a) Để A,B có nghĩa \(\Leftrightarrow\begin{cases}x+2\ge0\\x-3\ge0\end{cases}\)\(\Leftrightarrow\begin{cases}x\ge-2\\x\ge3\end{cases}\)\(\Leftrightarrow x\ge3\)
b) Có: A=B
\(\Leftrightarrow\sqrt{x+2}\cdot\sqrt{x-3}=\sqrt{\left(x-2\right)\left(x+3\right)}\)
\(\Leftrightarrow\sqrt{\left(x+2\right)\left(x-3\right)}-\sqrt{\left(x+2\right)\left(x-3\right)}=0\)
\(\Leftrightarrow0x=0\) (thỏa mãn với mọi x thuộc ĐK)
Vậy với mọi \(x\ge3\) thì A=B
a) A có nghĩa khi \(\begin{cases}x+2\ge0\\x-3\ge0\end{cases}\) \(\Leftrightarrow x\ge3\)
B có nghĩa khi \(\left(x+2\right)\left(x-3\right)\ge0\) \(\Leftrightarrow\begin{cases}x+2\ge0\\x-3\ge0\end{cases}\) hoặc \(\begin{cases}x+2\le0\\x-3\le0\end{cases}\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x\ge3\\x\le-2\end{array}\right.\)
b) Để A = B tức là cả A và B đều có nghĩa , suy ra đkxđ \(x\ge3\)
Vậy với mọi \(x\ge3\) thì A = B

\(A=\frac{\sqrt{x}-3}{\sqrt{x}-2}-\frac{2\sqrt{x}-1}{\sqrt{x}-1}+\frac{x-2}{x-3\sqrt{x}+2}\)
\(A=\frac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}-\frac{\left(2\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\) \(+\frac{x-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\)
\(A=\frac{x-4\sqrt{x}+3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}-\frac{2x-5\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\) \(+\frac{x-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\)
\(A=\frac{x-4\sqrt{x}+3-2x+5\sqrt{x}-2+x-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\)
\(A=\frac{\sqrt{x}-1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\)
\(A=\frac{1}{\sqrt{x}-2}\)
vậy \(A=\frac{1}{\sqrt{x}-2}\)
A có nghĩa khi \(\sqrt{x}-2>0\)
\(\Leftrightarrow\sqrt{x}=2\)
\(\Leftrightarrow x=4\)
vậy \(x=4\) thì A có nghĩa
b) theo ý a) \(A=\frac{1}{\sqrt{x}-2}\)
theo bài ra \(A>2\) \(\Leftrightarrow\frac{1}{\sqrt{x}-2}>2\)
\(\Leftrightarrow\frac{1}{\sqrt{x}-2}-2>0\)
\(\Leftrightarrow\frac{1}{\sqrt{x}-2}-\frac{2\left(\sqrt{x}-2\right)}{\sqrt{x}-2}>0\)
\(\Leftrightarrow\frac{1-2\sqrt{x}+4}{\sqrt{x}-2}>0\)
\(\Leftrightarrow\frac{5-2\sqrt{x}}{\sqrt{x}-2}>0\)
\(\Rightarrow\hept{\begin{cases}5-2\sqrt{x}>0\\\sqrt{x}-2>0\end{cases}}\) hoặc \(\hept{\begin{cases}5-2\sqrt{x}< 0\\\sqrt{x}-2< 0\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}-2\sqrt{x}>-5\\\sqrt{x}>2\end{cases}}\) hoặc \(\hept{\begin{cases}-2\sqrt{x}< -5\\\sqrt{x}< 2\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x< \frac{25}{4}\\x>4\end{cases}}\)hoặc \(\hept{\begin{cases}x>\frac{25}{4}\\x< 4\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}4< x< \frac{25}{4}\\x\notin\varnothing\end{cases}}\)
vậy \(4< x< \frac{25}{4}\) thì \(A>2\)

a) Giá trị của x để biểu thức có nghĩa:
\(\sqrt{\frac{-5}{-x-7}}\ne0\Leftrightarrow\frac{-5}{-x-7}\ne0\Leftrightarrow-x-7\ne0\Leftrightarrow x\ne-7\)
b) Giá trị của x để biểu thức có nghĩa:
\(\sqrt{x^2+2x+3}\ne0\Leftrightarrow x^2+2x+1\ne-2\Leftrightarrow\left(x+1\right)^2\ne-2\Leftrightarrow x+1\ne-\sqrt{2}\Leftrightarrow x\ne-\sqrt{2}-1\)