Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình như bạn nhầm nơi rồi đấy đây là BOX Lí mà đăng HÓA


1. Lấy ví dụ minh họa đồ thị hình 9.3 (SGK tr. 41).
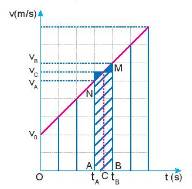
Ta sẽ tính độ dịch chuyển \(d\) của chất điểm có đồ thị vận tốc - thời gian như hình 9.3 trên.
Như đã biết theo đầu bài, độ dịch chuyển của chất điểm có độ lớn bằng với diện tích hình thang giới hạn bởi đồ thị (v - t) và trục tọa độ Ov, Ot.
Từ đồ thị, ta thấy được đáy nhỏ của hình thang có độ lớn là \(v_0\), đáy lớn của hình thang có độ lớn là \(v\) và chiều cao của hình thang có độ lớn là thời gian \(t\).
Công thức tính diện tích hình thang là: \(S=\dfrac{1}{2}\left(a+b\right)h\) với \(a,b,h\) lần lượt là độ dài đáy nhỏ, đáy lớn và chiều cao.
Áp dụng vào bài toán, ta được: \(d=S=\dfrac{1}{2}\left(v+v_0\right)t\)
\(=\dfrac{1}{2}vt+\dfrac{1}{2}v_0t\).
Mà: \(v=v_0+at\), thay vào ta được:
\(d=\dfrac{1}{2}\left(v_0+at\right)t+\dfrac{1}{2}v_0t\)
\(\Rightarrow d=\dfrac{1}{2}v_0t+\dfrac{1}{2}at^2+\dfrac{1}{2}v_0t\)
\(\Rightarrow d=v_0t+\dfrac{1}{2}at^2\) (điều phải chứng minh).
2. Ta có: \(\left\{{}\begin{matrix}v=v_0+at\\d=v_0t+\dfrac{1}{2}at^2\end{matrix}\right.\)
\(\Rightarrow v^2-v_0^2=\left(v+v_0\right)\left(v-v_0\right)\)
\(=\left(v_0+at+v_0\right)\left(v_0+at-v_0\right)\)
\(=at\left(2v_0+at\right)\)
\(=2a\left(v_0t+\dfrac{1}{2}at^2\right)=2ad\) (điều phải chứng minh).

a) PT x1 có dạng tổng quát là: \(x=x_0+v_0t+\dfrac{1}{2}at^2\) nên chuyển động của vật 1 là chuyển động thẳng biến đổi đều.
Căn cứ theo phương trình ta có:
+ \(x_0=0\)
+ \(v_0=-8(m/s)\)
+ \(a=2(m/s^2)\)
Do \(v_0<0\) nên t = 0 thì vật chuyển động ngược chiều dương của trục toạ độ.
Do \(v_0\) ngược dấu với \(a\) nên chuyển động đang là chuyển động chậm dần đều.
PT x2 có dạng tổng quát: \(x=x_0+v.t\) nên chuyển động của vật 1 là chuyển động thẳng đều, căn cứ theo phương trình ta suy ra được:
+ \(x_{02}=12(m)\)
+ \(v_2=5(m/s)\)
Do \(v_2>0\) nên vật 2 đang chuyển động cùng chiều dương với trục toạ độ.
b) Khoảng cách 2 vật là:
\(\Delta x = |x_1-x_2|=|t_2-13t-12|\)
\(t=2(s)\) \(\Rightarrow \Delta x = |2-13.2-12|=36(m)\)
c) Pt vận tốc của vật 2 là:
\(v=v_0+a.t=-8+2.t\) (m/s)
Vật 2 đổi chiều chuyển động khi \(v=0\Rightarrow -8+2.t=0\Rightarrow t = 4(s)\)
Ban đầu, t= 0 thì vị trí vật 2 là: \(x_2=12+5.0=12(m)\)
Khi t = 4s thì vị trí vật 2 là: \(x_2'=12+5.4=32(m)\)
Quãng đường vật 2 đi được là: \(S_2=x_2'-x_2=43-12=20(m)\)
d) Lúc t = 3s, vận tốc vật 1 là: \(v_1=-8+2.3=-2(m/s)\)
Lúc này vật 1 có vận tốc là 2m/s và đang chuyển động chậm dần đều ngược chiều dương của trục toạ độ. Còn vật 2 vẫn đang chuyển động đều với vận tốc là 5m/s theo chiều dương trục toạ độ.
e) Lúc t = 6s, vận tốc vật 1 là: \(v_1=-8+2.6=4(m/s)\)
Lúc này vật 1 có vận tốc là 4m/s và đang chuyển động nhanh dần đều cùng chiều dương của trục toạ độ. Còn vật 2 vẫn đang chuyển động đều với vận tốc là 5m/s theo chiều dương trục toạ độ.
f) Quãng đường vật 1 đi được từ 2s đến 5s là:
\(|(5^2-8.5)-(2^2-8.2)|=3(m)\)
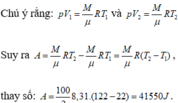
Đáp án: A
Công của khí:
Chú ý rằng:
Suy ra: