Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(m_nc_n\left(25-20\right)=m_{Al}c_{Al}\left(100-25\right)\)
=> \(m_n.4200.5=0,15.880.75\)
=> mn = 33/70 \(\approx0,47kg\)
Tính áp suất p' của khí trong bình .
Lúc đầu khí trong bình (1) có \(\begin{cases}V_1\\p=10^5Pa\\T=300K\end{cases}\) bình (2) có: \(\begin{cases}V_2=2V_1\\p\\T\end{cases}\)
Số mol khí trong hai bình \(n=\frac{3pV_1}{RT}\)
Lúc sau, khí trong bình (1) có \(\begin{cases}V_1\\p'\\T_1=273K\end{cases}\) bình (2) có \(\begin{cases}V_2=2V_1\\p'\\T_2=330K\end{cases}\)
Số mol khí trong bình (1): \(n_1=\frac{p'V_1}{RT_1}\), trong bình (2): \(n_2=\frac{2p'V_1}{RT_2}\)
\(n=n_1+n_2\Leftrightarrow\frac{3pV_1}{RT}=\frac{p'V_1}{RT_1}+\frac{2p'V_2}{RT_2}\)
\(\frac{3p}{T}=p'\left(\frac{1}{T_1}+\frac{2}{T_2}\right)\) suy ra \(p'=1,024.10^5Pa\)
m1=100g=0,1kg
m2=300g=0,3kg
m3=75kg=0,075
gọi t là nhiệt độ cân bằng
\(Q_{tỏa}+Q_{thu}=0\)
\(m_1.c_{Al}.\left(t_1-t\right)+m_2.c_{H_2O}.\left(t_1-t\right)+m_3.c_{Cu}.\left(t_2-t\right)=0\)
\(\Rightarrow t\approx21,66^0C\)
Ta có:
∆E = -4,176.10-13 J = -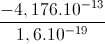 
= -2,61 MeV.
=> KP = Kn =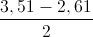 
= 0,45 MeV
Mặt khác ta có:
K =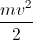 
nên v = 
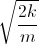và 931 MeV/u = 1c2
Vậy: vP =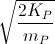 
= 1,7.106 m/s.
m n = 1,0087u
ban đầu có 1 hạt n, sau sinh ra 2 hạt n
=> m hao hụt = m U + m n - m Mo- m La - 2 . m n = 0,23u
=> năng lượng tỏa = 0,23 . 931 = 214 M ev
1. Lấy ví dụ minh họa đồ thị hình 9.3 (SGK tr. 41).
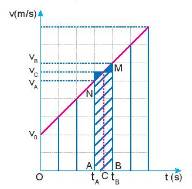
Ta sẽ tính độ dịch chuyển \(d\) của chất điểm có đồ thị vận tốc - thời gian như hình 9.3 trên.
Như đã biết theo đầu bài, độ dịch chuyển của chất điểm có độ lớn bằng với diện tích hình thang giới hạn bởi đồ thị (v - t) và trục tọa độ Ov, Ot.
Từ đồ thị, ta thấy được đáy nhỏ của hình thang có độ lớn là \(v_0\), đáy lớn của hình thang có độ lớn là \(v\) và chiều cao của hình thang có độ lớn là thời gian \(t\).
Công thức tính diện tích hình thang là: \(S=\dfrac{1}{2}\left(a+b\right)h\) với \(a,b,h\) lần lượt là độ dài đáy nhỏ, đáy lớn và chiều cao.
Áp dụng vào bài toán, ta được: \(d=S=\dfrac{1}{2}\left(v+v_0\right)t\)
\(=\dfrac{1}{2}vt+\dfrac{1}{2}v_0t\).
Mà: \(v=v_0+at\), thay vào ta được:
\(d=\dfrac{1}{2}\left(v_0+at\right)t+\dfrac{1}{2}v_0t\)
\(\Rightarrow d=\dfrac{1}{2}v_0t+\dfrac{1}{2}at^2+\dfrac{1}{2}v_0t\)
\(\Rightarrow d=v_0t+\dfrac{1}{2}at^2\) (điều phải chứng minh).
2. Ta có: \(\left\{{}\begin{matrix}v=v_0+at\\d=v_0t+\dfrac{1}{2}at^2\end{matrix}\right.\)
\(\Rightarrow v^2-v_0^2=\left(v+v_0\right)\left(v-v_0\right)\)
\(=\left(v_0+at+v_0\right)\left(v_0+at-v_0\right)\)
\(=at\left(2v_0+at\right)\)
\(=2a\left(v_0t+\dfrac{1}{2}at^2\right)=2ad\) (điều phải chứng minh).
Hình như bạn nhầm nơi rồi đấy đây là BOX Lí mà đăng HÓA