Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

30 0 h
Bài này có 2 cách giải, mình dùng định luật bảo toàn cho nhanh.
Chọn mốc thế năng ở chân mặt phẳng nghiêng.
Độ cao mặt phẳng nghiêng: \(h=10.\sin 30^0=5(m)\)
Ở đỉnh mặt phẳng nghiêng, cơ năng của vật: \(W_1=mgh\)
Ở chân mặt phẳng nghiêng, cơ năng là: \(W_2=\dfrac{1}{2}mv^2\)
Bảo toàn cơ năng: \(W_1=W_2\Rightarrow mgh=\dfrac{1}{2}mv^2\Rightarrow v=\sqrt{2gh}=\sqrt{2.10.5}=10(m/s)\)

Chọn mốc thế năng tại mặt đất
a) Động năng lúc ném: \(W_đ=\dfrac{1}{2}mv^2=\dfrac{1}{2}.1.3^2=4,5(J)\)
Thế năng: \(W_t=mgh=1.10.1,5=15(J)\)
b) Ở vị trí cao nhất vận tốc bằng 0 nên động năng bằng 0
Cơ năng: \(W=W_đ+W_t=4,5+15=19,5(J)\)
c) Ở vị trí cao nhất, thế năng bằng cơ năng
\(\Rightarrow mg.h_{max}=19,5\Rightarrow h_{max}=1,95m\)

Dòng điện xoay chiều khiến cho dây chịu tác dụng của lực từ, và sẽ dao động theo phương vuông góc với đường sức từ, với tần số 50Hz, hay ω=2πf=100πω=2πf=100π và T=0.02sT=0.02s
Khoảng cách giữa 2 điểm dừng (ứng với 1 bụng sóng) là λ/2=vT/2=12×0.02/2=0.12λ/2=vT/2=12×0.02/2=0.12
Có 6 bụng sóng, vậy thì chiều dài sợi dây là: 6λ2=0.12×6=0.72(m)6λ2=0.12×6=0.72(m)
Đáp án là A. 72cm

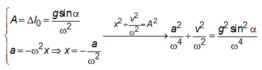
Điểm tiếp xúc \(I\) là tâm quay tức thời.\(\widehat{AMI}\) là góc vuông. Vận tốc \(\overrightarrow{v}\) của M vuông góc với IM nên góc \(\beta\) mà \(\overrightarrow{v}\) làm phương nằm ngang là \(\beta=\widehat{AMI}=\frac{\alpha}{2}\) Lăn không trượt có nghĩa là:
Cung \(IP=IP'=OO'\). Trong 1 đơn vị thời gian ta có \(R\omega=v_0\left(1\right)\), \(\omega\) là vận tốc quay nhanh O. Vận tốc góc của vật rắn chuyển động phẳng không phụ thuộc vào trục quay: A và M quay quanh \(I\).
Vậy \(v_A=2R\omega\left(2\right)\);\(v=\omega2R\cos\frac{\alpha}{2}\). Suy ra \(\omega=\frac{v}{2R\cos\frac{\alpha}{2}}\)
Thay vào (1),(2) ta có \(v_0,v_A\) theo \(v\).
\(v_0=\frac{v}{2\cos\frac{\alpha}{2}};v_A=\frac{v}{\cos\frac{\alpha}{2}}\)

a)Chọn gốc thế năng tại mặt đất( điểm O)a) Gọi vị trí ném là A ,
\(W_A=\frac{1}{2}mv^0_2+mgh=\frac{1}{2}.0,1.10^2+0,1.10.10=15J\)
b)Gọi điểm cao nhất mà vật có thể đạt đk là : B
Cơ năng của vật tại B là : \(W_B=mg.OB\)
ADĐLBTCN : \(W_A=W_B\)
<=> mg.OB=15
<=> OB=15 (m)
c) Vận tốc khi chạm đất là :
\(V_đ=\sqrt{2g.OB}=\sqrt{2.10.15}\approx17,32\left(m\text{ /}s\right)\)
d) Gọi vị trí mà động năng =3/2 thế năng là D : \(W_đ=3\text{/}2W_t\)
-Cơ năng tại D là : \(W_D=W_t+W_đ=5\text{/}2W_t=5\text{/}2.mg.OD\)
ADĐLBTCN : \(W_A=W_D\)
<=> 5/2.mg.OD=15
<=> OD=6 (m)
Vậy : ....
Vậy độ cao cực đại mà vật đạt đk là 15m
a) Chọn gốc thế năng tại mặt đất (1)
Vị trí ném (2)
Ta có: \(W_2=\frac{1}{2}mv_2^2+mgz=\frac{1}{2}.0,1.10^2+0,1.10.10=15J\)
b) Độ cao cực đại vật đạt được (3)
Ta có: \(W_2=\frac{1}{2}mv_2^2\)
\(W_3=mgz_3\)
Áp dụng định luật bảo toàn cơ năng:
\(W_2=W_3\)
\(\Leftrightarrow\frac{1}{2}mv_2^2=mgz_3\)
\(\Rightarrow z_3=\frac{v_2^2}{2g}=5m\)
Độ cao cực đại mà vật đạt được so với mặt đất: 10+5=15m
c) Ta có: \(W_1=\frac{1}{2}mv_1^2\)
\(W_3=mgz_3\)
Áp dụng định luật bảo toàn cơ năng:
\(W_1=W_3\)
\(\Leftrightarrow\frac{1}{2}mv_1^2=mgz_3\)
\(\Rightarrow v_1=\sqrt{2gz_3}=10\sqrt{3}\)(m/s)
d) Vị trí mà \(W_đ=\frac{3}{2}W_t\) (4)
Ta có: \(W_4=W_{đ_4}+W_{t_4}\)
Áp dụng định luật bảo toàn cơ năng:
\(W_4=W_2\)
\(\Leftrightarrow W_{đ_4}+W_{t_4}=15\)
\(\Leftrightarrow\frac{3}{2}W_{t_4}+W_{t_4}=15\)
\(\Leftrightarrow\frac{5}{2}mgz_4=15\)
\(\Leftrightarrow z_4=6\left(m\right)\)

ta có:f=4p/2p=2(hz)
lamda=v/f=50/2=25(cm)
vì M cùng pha với O nên :2p*d1/lamda=2p suy ra d1=25(cm)
vì N ngược pha với O nên :2p*d2/lamda=p suy ra d2 =12.5(cm)

Đáp án B
Ta có x = 400 t , y = 5 t 2 ; khi viên đạn rơi vào sườn đồi ta có y x = tan 30 0 = 1 3
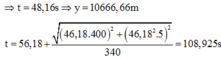


Đáp án B
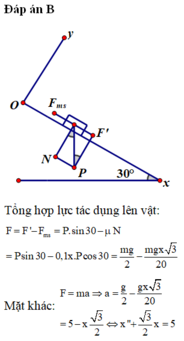
Chọn mốc tính thế năng ở chân mặt phẳng nghiêng.
Cơ năng của vật bảo toàn nên cơ năng ở đỉnh mặt phẳng nghiêng = Cơ năng ở chân mặt phẳng nghiêng
Ta có: mglsin 60 o = 0,5m v 2
Thay số: 10.10.sin 60 o = 0,5. v 2 => v = 10m/s