Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

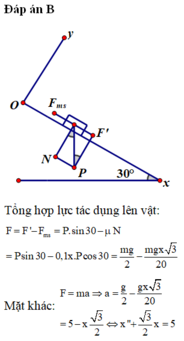
Đáp án B
Chọn mốc tính thế năng ở chân mặt phẳng nghiêng.
Cơ năng của vật bảo toàn nên cơ năng ở đỉnh mặt phẳng nghiêng = Cơ năng ở chân mặt phẳng nghiêng
Ta có: mglsin 60 o = 0,5m v 2
Thay số: 10.10.sin 60 o = 0,5. v 2 => v = 10m/s

Chọn đáp án B
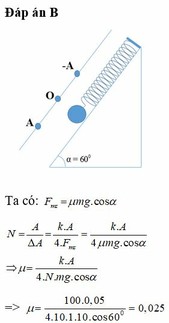
Sau 10 dao động vật dừng lại như vậy có 20 lần qua VTCB
Độ giảm biên độ của vật sau một lần qua VTCB: Δ N = A N = 0 , 05 20 = 2 , 5.10 − 3 m
Mặt khác vật dao động tắt dần trên mặt phẳng nghiên nên ta có độ giảm biên độ sau một lần vật qua VTCB: 2 μ m g cos α k = 2 , 5.10 − 3 ⇒ u = 2 , 5.10 − 2

Đáp án C.
Ta có:
![]()
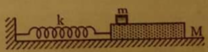
Độ giảm biên độ trong một chu kì:
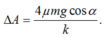
Số dao động từ lúc bắt đầu đến lúc dừng lại:
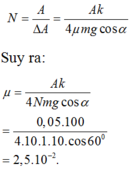

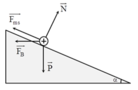
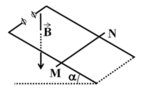
+ Áp dụng quy tắc bàn tay trái ta xác định được chiều của lực từ như hình vẽ.
+ Áp dụng định luật II Niuton ta có:
mgsina - Fms - FB.cosa = ma
+ Ta lại có:
* FB = B.I.l
* Fms = m.N = m.(mgcosa + FB.sina)
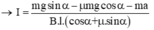
+ Thay các giá trị m = 0,16;
m = 0,4; a = 0,2; g = 10;
a = 300; l = 1; B = 0,05 vào phương trình trên ta được: I » 4 A
Đáp án D

Chọn B
Áp dụng định luật bảo toàn và chuyển hóa cơ năng ở hai vị trí chân dốc và ở vị trí đầu dốc
E 1 − E 0 = μ 1 m g S 1 → S t = 0 1 2 m v 0 2 ⏟ E 0 = 1 2 m v 2 + m g h ⏟ E 1 ⇒ v = v 0 2 − 2 g h
Áp dụng định luật bảo toàn và chuyển hóa cơ năng ở hai vị trí đầu dốc và vị trí vật dừng lại
0 − 1 2 m v 2 = − μ 2 m g . S 2 ⇒ S 2 = v 2 2 μ g = v 0 2 − 2 g h 2 μ g = 4 m




30 0 h
Bài này có 2 cách giải, mình dùng định luật bảo toàn cho nhanh.
Chọn mốc thế năng ở chân mặt phẳng nghiêng.
Độ cao mặt phẳng nghiêng: \(h=10.\sin 30^0=5(m)\)
Ở đỉnh mặt phẳng nghiêng, cơ năng của vật: \(W_1=mgh\)
Ở chân mặt phẳng nghiêng, cơ năng là: \(W_2=\dfrac{1}{2}mv^2\)
Bảo toàn cơ năng: \(W_1=W_2\Rightarrow mgh=\dfrac{1}{2}mv^2\Rightarrow v=\sqrt{2gh}=\sqrt{2.10.5}=10(m/s)\)
444