Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tóm tắt:
\(m=4kg\)
\(t=2,5s\)
____________________________
\(\Delta p=?kg.m/s\)
Giải:
Rơi tự do ko vận tốc đầu nên v1=0
Vận tốc ở tg 2s:
\(v_2=g.t=10.2,5=25\left(m/s\right)\)
Độ biến thiên động lượng của vật:
\(\Delta p=p_2-p_1=m.\left(v_2-v_1\right)=4.\left(25-0\right)=100\left(kg.m/s\right)\)
Vậy ...

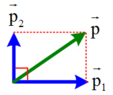
+ Vì v → 2 chếch lên trên, hợp với v → 1 góc 90 ° vuông góc
⇒ p = p 1 2 + p 2 2 = 8 2 + 6 2 = 10 k g . m / s
Chọn đáp án C

Vì vật chuyển động đều
\(\Rightarrow\overrightarrow{F}+\overrightarrow{N}+\overrightarrow{P}+\overrightarrow{F_{ms}}=\overrightarrow{0}\)
Chọn trục toạ độ có trục hoành hướng sang phải, trục tung hướng lên
\(\Rightarrow\left\{{}\begin{matrix}Ox:F.\cos\alpha-F_{ms}=0\\Oy:F.\sin\alpha+N-P=0\end{matrix}\right.\)
\(\Rightarrow F.\cos\alpha-\mu.\left(P-F.\sin\alpha\right)=0\)
\(\Leftrightarrow120.\cos60-\mu.\left(200-120.\sin60\right)=0\)
=> \(\mu=...\)
Tìm gia tốc trong trường hợp alpha= 300 thì lúc này vật chuyển động biến đổi đều nên có gia tốc, tức là \(\overrightarrow{F}+\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_{ms}}=m.\overrightarrow{a}\)
Cậu chiếu lên trục toạ độ rồi phân tích, bt hệ số ma sát rồi thì tìm a ez

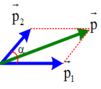
+ Vì v 2 → hướng chếch lên trên hợp với v 1 → góc 60 ° nên p → 1 ; p → 2 tạo với nhau một góc 60 °
⇒ p 2 = p 1 2 + p 2 2 + 2 p 1 p 2 cos α
⇒ p = 8 2 + 6 2 + 2.8.6 cos 60 0 = 2 37 k g . m / s
Chọn đáp án D

a)
Chọn chiều (+) hướng lên. Gốc thời gian lúc bắt đầu ném
\(y=v_0t+\frac{gt2}{2}=20t-5t^2\) (1)
\(v=v_0+gt=20-10t\) (2)
Tại điểm cao nhất v=0
Từ (2) \(\Rightarrow\) t=2(s) thay vào (1)
yM = 20(m)
b)
Khi chạm đất y=0 từ (1)\(\Rightarrow\) t=0 và t=4 (s)
Thay t = 4 (s) vào (2) \(v'=-20m\text{/}s\)
(Dấu trừ (-) vận tốc ngược với chiều dương.)

Câu 2: Một người kéo một thùng nước có khối lượng 15kg từ giếng sâu h=8m lên, chuyển động nhanh dần đều trong 4s. lấy \(g=10m/s^2\) Tính công và công suất của người đó.
_______________________________________________
\(h=\frac{1}{2}at^2\)
\(8=\frac{1}{2}a.4^2\)
\(a=1m/s\)
\(F-P=ma\)
\(F=ma+P=15.1+15.10=165N\)
\(A=Fs=165.8=20,625J\)
\(P=\frac{A}{t}=\frac{20,625}{4}=5,15625W\)
Vậy ............
Câu 1
\(p=\sqrt{p_1^2+P_2^2}=\sqrt{\left(1.3\right)^2+\left(4.1\right)^2}=5\)
Câu 2
\(m=15\left(kg\right)\)
\(h=S=8m\)
\(t=4s\)
\(g=10\left(\frac{m}{s^2}\right)\)
a. Tính A = ?
Quãng đường mà thùng nước đi được :
\(S=\frac{1}{2}at^2\rightarrow a=\frac{2S}{t^2}=\frac{2.8}{4^2}=1\left(\frac{m}{s^2}\right)\)
Theo định luật II Niuton ta có : vectoP + vectoF = m.vecto a
\(\rightarrow F=P+ma\)
\(\rightarrow F=mg+ma\)
\(\rightarrow F=15.10+15,1=165\left(N\right)\)
- Công của lực kéo tính theo công thức : \(A=F.S\)
\(\rightarrow A=F.S\)
\(\rightarrow A=165.8=1320\left(J\right)\)
b . Tính: P = ?
- Công suất của người ấy tính theo công thức : \(P=\frac{A}{t}\)
\(\rightarrow P=\frac{1320}{4}=330\left(W\right)\)

Ta có:
p → = p → 1 + p → 2 v à p 1 = m 1 . v 1 = 2.4 = 8 ( k g . m / s ) ; p 2 = m 2 . v 2 = 3.2 = 6 ( k g . m / s )
a. Vì v → 2 cùng hướng với v 1 → ⇒ p → 1 , p → 2 cùng phương, cùng chiều
⇒ p = p 1 + p 2 = 8 + 6 = 14 ( k g . m / s )
![]()
b. Vì v → 2 ngược hướng với v 1 → ⇒ p → 1 , p → 2 cùng phương, ngược chiều
⇒ p = p 1 − p 2 = 8 − 6 = 2 ( k g . m / s )
![]()
c. Vì v → 2 hướng chếch lên trên, hợp với v 1 → góc 900 ⇒ p → 1 , p → 2 vuông góc
⇒ p = p 1 2 + p 2 2 = 8 2 + 6 2 = 10 ( k g . m / s )
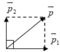
d. Vì v → 2 hướng chếch lên trên, hợp với góc 600 ⇒ p → 1 , p → 2 tạo với nhau một góc 60 o
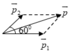
⇒ p 2 = p 1 2 + p 2 2 + 2 p 1 p 2 cos α ⇒ p = 8 2 + 6 2 + 2.8.6 cos 60 0 = 2 37 ( k g . m / s )
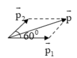

+ Vì v → 2 hướng chếch lên trên hợp với v → 2 góc 60 ° nên p → 1 ; p → 2 tạo với nhau một góc 60 °
⇒ p 2 = p 1 2 + p 2 2 + 2 p 1 p 2 cos α
⇒ p = 8 2 + 6 2 + 2.8.6 cos 60 0 = 2 37 k g . m / s
Chọn đáp án B