Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: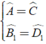
⇒ Δ CDB ∼ Δ ABE ( g - g )
⇒ CD/AB = BC/AE
hay CD/15 = 10/12 ⇔ CD = (10.15)/12 ⇒ CD = 18 ( cm )
Áp dụng định lý Py – ta – go vào tam giác vuông ABE có:


a)
![]()
Vậy ∠EBD = 900
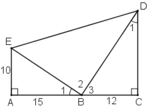
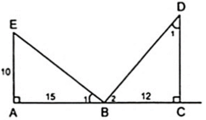
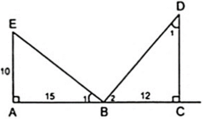
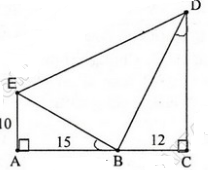
Vậy trong hình vẽ có ba tam giác vuông đó là:
∆ABE, ∆CBD, ∆EBD.
b) ∆ABE và ∆CDB có:
∠A = ∠C = 900
∠ABE = ∠CDB
=> ∆ABE ∽ ∆CDB => AB/CD = AE/CB
=> CD = AB.CB/AE
= 18 (cm)
∆ABE vuông tại A => BE =
![]() = 18 cm
= 18 cm
∆EBD vuông tại B => ED =
![]()
= 28,2 cm
c) Ta có: ![]()
= 1/2 . 10.15 + 1/2 . 12.18
= 75 + 108 = 183 cm2
SACDE = 1/2 (AE + CD).AC =1/2 (10+18).27=378 cm2
=> SEBD = SEBD – ( SABE + SDBC) = 378 – 183 = 195cm2

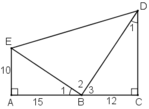
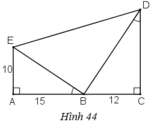
a) + ΔABE vuông tại A.
+ ΔBCD vuông tại C.
+ Ta có:
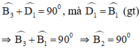
Vậy ΔBED vuông tại B.
b) + Áp dụng định lý Pytago trong ΔABE vuông tại A ta có:
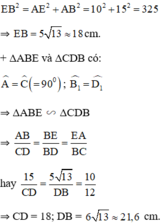
+ Áp dụng định lý Pytago trong ΔEBD vuông tại B ta có:
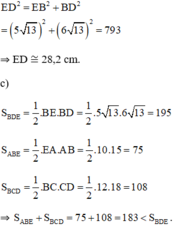

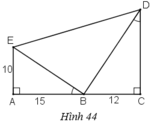
a) + ΔABE vuông tại A.
+ ΔBCD vuông tại C.
+ Ta có:
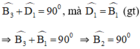
Vậy ΔBED vuông tại B.
b) + Áp dụng định lý Pytago trong ΔABE vuông tại A ta có:
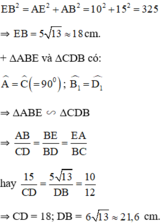
+ Áp dụng định lý Pytago trong ΔEBD vuông tại B ta có:
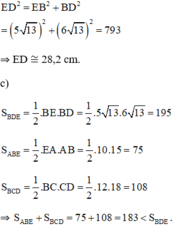

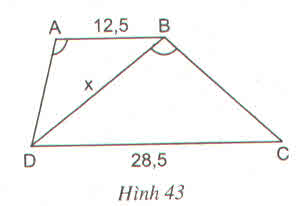
Xét ∆ABD và ∆BDC có:

=> ∆ABD ∽ ∆BDC(trường hợp 3)

=> BD = √(AB.DC) = √(12,5.8,5) = √356,25 => BD = 18,9 cm
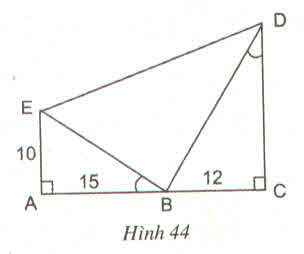


Ta có: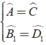
⇒ Δ CDB ∼ Δ ABE ( g - g )
⇒ CD/AB = BC/AE hay CD/15 = 10/12 ⇔ CD = ( 10.15)/12 ⇒ CD = 18 ( cm )
Áp dụng định lý Py – ta – go vào tam giác vuông ABE có: