Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tứ giác ABDC có hai đường chéo cắt nhau tại trung điểm mỗi đường ⇒ ABDC là hình bình hành
Hình bình hành ABDC có hai đường chéo bằng nhau ⇒ ABDC là hình chữ nhật
b) ABDC là hình chữ nhật ⇒ góc BAC = 90o
⇒ ΔABC là tam giác vuông tại A
c) Định lí: Tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác đó là tam giác vuông

1/ a/ BC = \(\sqrt{5^2+12^2}\)= 13 (cm) (định lí Pytago)
Vì AM là đường trung tuyến ứng với cạnh BC nên AM = 1/2 BC = 1/2 x 13 = 6,5 (cm)
b/ Ta có: \(\widehat{DAE}=\widehat{MDA}=\widehat{MEA}=\)90 độ
=> Tứ giác ADME là hình chữ nhật
c/ AM là phân giác của \(\widehat{BAC}\)
[ học toán ngu nhất là cm câu c :"< mấy câu giống vậy anh bỏ hết ]

A B C M D E 8 6
a) ADME là hình gì?
tứ giác ADME có:
\(\widehat{A}=90^o\)(Tam giác ABC vuông tại A)
\(\widehat{MDA}=90^o\)(\(MD\perp AB\))
\(\widehat{MEA}=90^o\)(\(ME\perp AC\))
Suy ra ADME là hình chữ nhật.
b) Tìm điều kiện của tam giác ABC để ADME là hình vuông
Hình chữ nhật ADME là hình vuông
\(\Leftrightarrow\)AM là phân giác \(\widehat{DAE}\)hay AM là phân giác \(\widehat{BAC}\)
mà AM là trung tuyến của tam giác vuông ABC
\(\Rightarrow\Delta ABC\)vuông cân tại A.
c) tính AM?
Áp dụng định lý pytago vào tam giác ABC
có \(BC^2=AB^2+AC^2=6^2+8^2=100\)
\(\Rightarrow BC=\sqrt{100}=10\left(cm\right)\)
Vì AM là đường trung tuyến ứng với cạnh huyền BC của tam giác vuông ABC nên \(AM=\frac{BC}{2}=\frac{10}{2}=5\left(cm\right)\)
d) Tính \(S_{ABM}\)?
tam giác ABC có M trung điểm BC mà ME // AD (ADME hình chữ nhật) hay ME // AB
=> ME là đường trung bình tam giác ABC
=> E trung điểm AC
\(\Rightarrow AE=\frac{AC}{2}=\frac{6}{2}=3\left(cm\right)\)
mà DM = AE (ADME là hcn)
\(\Rightarrow AE=DM=3\left(cm\right)\)
\(\Rightarrow S_{ABM}=\frac{1}{2}.AB.DM=\frac{1}{2}.8.3=12\left(cm^2\right)\)
ĐS:...........
(Thời gian hoàn thành 9:37 PM)

Xét \(\Delta\)ABC có: D là trung điểm của AB
M là trung điểm của BC
\(\Rightarrow\)DM là đường trung bình của \(\Delta ABC\)
\(\Rightarrow DM\)//AC hay DM//AE
Ta có : M là trung điểm của BC
E là trung điểm của CA
\(\Rightarrow\)ME là đường trung bình của \(\Delta\)ABC
\(\Rightarrow\)ME//AB hay ME//AD
Xét tứ giác ADME có: DM//AE(cmt)
ME//AD(cmt)
\(\Rightarrow\)ADME là hình bình hành
Nếu \(\Delta\)ABC cân tại A có đường trung tuyến AM
\(\Rightarrow\)AM đồng thời là tia phân giác của \(\widehat{A}\)
Xét hình bình hành ADME có đường chéo AM là tia phân giác của \(\widehat{A}\)(cmt)
\(\Rightarrow\)ADME là hình thoi
Nếu \(\Delta\)ABC vuông tại A
\(\Rightarrow\widehat{A}=90^0\)
Xét hình bình hành ADME có \(\widehat{A}=90^0\)(cmt)
\(\Rightarrow\)ADME là hình chữ nhật
d/ Xét \(\Delta ABC\) vuông tại A, đường trung tuyến AM
\(\Rightarrow AM=\frac{1}{2}BC\)(Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền thì bằng 1/2 cạnh huyền)
Áp dụng định lí Py-ta-go vào tam giác ABC vuông tại A ta có:
BC2=AB2+AC2
\(\Leftrightarrow BC=\sqrt{AB^2+AC^2}\)
\(\Leftrightarrow BC=\sqrt{6^2+8^2}\)
\(\Leftrightarrow BC=10\left(cm\right)\)
Khi đó:AM=\(\frac{1}{2}.BC=\frac{1}{2}.10=5\left(cm\right)\)
Vậy trong trường hợp tam giác ABC vuông tại A, AB=6cm và AC=8cm thì AM=5cm

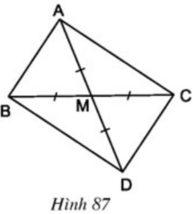
a) Xét tứ giác ABCD có:
. M là trung điểm của BC ( AM là đường trung tuyến)
. M là tđ của AD ( gt)
Vậy: ABCD là hbh ( tứ giác có 2 đường chéo cắt nhau tại tđ của mỗi đường)
mà \(\widehat{BAC}\) = 900 ( \(\Delta\) ABC vuông tại A)
--> ABCD là hình chữ nhật ( hbh có 1 góc vuông)
b) Ta có: \(IA\perp AC\)
\(CD\perp AC\)
\(\Rightarrow\) IA // CD
Xét tứ giác BIDC có:
. IA // CD (cmt)
\(\Rightarrow\) IB // CD ( B ϵ IA )
. AB =CD ( cạnh đối hcn ABCD )
mà AB = IB ( tính chất đối xứng)
\(\Rightarrow\) IB = CD ( cùng = AB )
Vậy: BIDC là hbh ( tứ giác có 2 cạnh đối vừa //, vừa = nhau)
\(\Rightarrow\) BC // ID ( cạnh đối hbh)
" đề câu c sai nha bạn"

Bài 1: Giải: Xét tam giác ACD có F,G lần lượt là trung điểm AC,DC nên FG là đường trung bình
\(\Rightarrow\)\(FG//AD\)
C/m tương tự đc \(EH//AD; GH//EF//BC\)
\(\Rightarrow EFGH\) là hình bình hành
a/Để EFGH là hình chữ nhật thì góc \(FGH=90^o\)
\(\Rightarrow góc HGD+góc FGC=90^o\)
Mà góc HGD=góc BCD;góc FGC= góc ADC ( góc đồng vị = nhau)
\(\Rightarrow\) góc BCD+góc ADC=\(90^o\)
\(\Rightarrow\)Để EFGH là hình chữ nhật thì tứ giác ABCD cần có góc BCD+góc ADC=\(90^o\)
b/Để EFGH là hình thoi thì FG=HG
Mà FG=1/2AD; HG=1/2BC
\(\Rightarrow\)AD=BC
\(\Rightarrow\)Để EFGH là hình thoi thì tứ giác ABCD có AD=BC
c/ để EFGH là hình vuông thì EFGH phải vừa là hình chữ nhật vừa là hình thoi\(\Rightarrow \)ABCD phải có đủ cả 2 điều kiện trên

Câu hỏi của Cỏ Bốn Lá - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo tại đây nhé.
ABCHMNPO
S ABC = \(\frac{1}{2}\)AH.BC=\(\frac{1}{2}\)AB.AC
suy ra : AH.BC=AB.AC
b) Tứ giác ANMP có \(\widehat{A}\)=\(\widehat{N}\)=\(\widehat{M}\)=90\(^0\)nên tứ giác ANMP là hình chữ nhật .
c) Gọi O là giao điểm hai đường chéo AM và NP của hình chữ nhật ANMP do đó O là trung điểm của đoạn AM và NP
tam giác AHM vuông tại H có HO là đường trung tuyến ứng với cạnh huyền AM nên HO =\(\frac{1}{2}\) AM = \(\frac{1}{2}\)NP (vì AM = NP ,hai đường chéo của hình chữ nhật ANMP )
Xét tam giác NHP có đường trung tuyến HO= \(\frac{1}{2}\)NP ,suy ra tam giác NHP vuông tại H
Vậy \(\widehat{NHP}\)= 90\(^0\)
d) Ta có : NP = AM ( Tính chất đường chéo hình chữ nhật )
NP nhỏ nhất khi AM nhỏ nhất
AM nhỏ nhất khi M trùng với H . Vậy NP nhỏ nhất khi M trung với H.
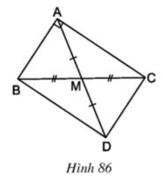
a) Tứ giác ABDC có hai đường chéo cắt nhau tại trung điểm mỗi đường ⇒ ABDC là hình bình hành
Hình bình hành ABDC có góc A vuông ⇒ ABDC là hình chữ nhật
b) Hình chữ nhật ABDC ⇒ AD = BC (hai đường chéo)
c) Định lí: Trong một tam giác vuông, trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền