Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a ) Ta co \(AC^2+BD^2=MA^2+MC^2+MB^2+MD^2\)
\(=\left(MA^2+MD^2\right)+\left(MB^2+MC^2\right)=AD^2+BC^2\)
Kẻ đường kính CE ta có \(\widehat{CDE}=90^0\)
Hay \(CD\perp DE\)
\(\Rightarrow DE\)// \(AB\) nên tứ giác ABED là hình thang cân
\(\Rightarrow AD=BE\)
Ta có : \(AD^2+BC^2=BE^2+BC^2=CE^2=4R^2\) không dổi
b ) Vì IB = IC = IM nên \(IO^2+IM^2=OC^2-IM^2+IM^2=R^2\)
Gọi J là trung điểm của MO . Áp dụng công thức đường trung tuyến trong \(\Delta IMO\) Ta có : \(IJ=\sqrt{\frac{IO^2+IM^2}{2}-\frac{MO^2}{4}}=\sqrt{\frac{R^2}{2}-\frac{MO^2}{4}}\) ( không dổi vì OM cố định ) Do đó I chạy trên đường tròn tâm J bán kính IJ không đổi Chúc bạn học tốt !!
Vì góc ACB là có nội tiếp chắn nửa đường tròn của (O)
=> góc ACB= 90 độ
Xét (I) có góc MCN là góc nội tiếp chắn cung MN
mà góc MCN= 90 độ
=> MN là đường kính của (I)
=> 3 điểm M,I,N thẳng hàng
b) vì Δ CIN cân tại I( IC=IN=R)
=> góc ICN= góc INC
lại có Δ COB cân tại O(OC=OB=R)
=> góc OCB= góc OBC
=> góc INC= góc OBC ( cùng = góc OCB)
mà 2 góc này ở vị trí đồng vị của 2 đường thẳng MN và AB
=> MN // AB
lại có ID vuông góc với AB
=> ID vuông góc với MN( đpcm)
a: Xét (O) có
CA là tiếp tuyến
CM là tiếp tuyến
DO đó: CA=CM và OC là tia phân giác của góc MOA(1)
Xét (O) có
DM là tiếp tuyến
DB là tiếp tuyến
Do đó:DM=DB và OD là tia phân giác của góc MOB(2)
Ta có: CM+MD=CD
nên CD=AC+BD
b: Từ (1) và (2) suy ra \(\widehat{COD}=\dfrac{1}{2}\cdot180^0=90^0\)
Xét ΔCOD vuông tại O có OM là đường cao
nên \(MC\cdot MD=OM^2\)
=>\(R^2=AC\cdot BD\)
1: Xét tứ giác ABOC có \(\widehat{ABO}+\widehat{ACO}=180^0\)
nên ABOC là tứ giác nội tiếp
2: \(OA=\sqrt{3^2+5^2}=\sqrt{34}\left(cm\right)\)
Xét ΔOBA vuông tại B có BH là đường cao
nên \(BH\cdot OA=BO\cdot BA\)
hay \(BH=\dfrac{15\sqrt{34}}{34}\left(cm\right)\)
=>\(BC=\dfrac{30\sqrt{34}}{34}\left(cm\right)\)
Đính chính lại nhé
\(\frac{BE}{AE}=\frac{1}{2}\) chứ không phải \(\frac{DE}{AE}\) nhé
chtt sẽ có câu a nhé bạn
câu b thì bạn thay góc vào là ra
còn câu c thì =))
1. Theo định lí Viet ta có :
\(\left[{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}=2\\x_1.x_2=\dfrac{c}{a}=-1\end{matrix}\right.\)
P = \(\left(x_1\right)^3+\left(x_2\right)^3=\left(x_1+x_2\right)^3-3x_1.x_2\left(x_1+x_2\right)\)
= \(2^3 - 3.(-1).2 = 8 + 6 = 14\)
2. Bạn tự vẽ hình nhé
a. Gọi N là trung điểm của AO
△ABO vuông tại B, trung tuyến BN có:
AN = BN = ON = \(\dfrac{1}{2}\)AO (1)
△ACO vuông tại C, trung tuyến CN có:
ON = BN = CN = \(\dfrac{1}{2}\)AO (2)
Từ (1) và (2) suy ra: AN = BN = ON = CN = \(\dfrac{1}{2}\)AO
=> Bốn điểm A,B,O,C cùng thuộc đường tròn (N)
=> Tứ giác ABOC nội tiếp hay N là tâm đường tròn ngoại tiếp tứ giác ABOC
b. Xét △ABD và △AEB có:
\(\widehat{BAE}\) chung
\(\widehat{ABD}=\widehat{AEB}\) (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn \(\stackrel\frown{BD}\))
=> △ABD ∼ △AEB
=> \(\dfrac{AD}{AB}=\dfrac{AB}{AE}\)
=> \(AB^2=AD.AE\)
c. Ta có:
\(\widehat{AHB}=\widehat{HMC}\) (đồng vị)
\(\widehat{HMC}=\widehat{ACB}\) (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn \(\stackrel\frown{BC}\))
\(\widehat{ACB}=\widehat{AOB}\) (tứ giác ABOC nội tiếp)
=> \(\widehat{AHB}=\widehat{AOB}\)
=> Tứ giác ABHO nội tiếp
Lại có: \(\widehat{ABO}=90^0\)
=> \(\widehat{AHO}=90^0\)
=> OH ⊥ DE (đường kính OH vuông góc với dây DE)
=> H là trung điểm của DE hay DH = DE
Vẽ Hình
b) Vì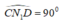
nên 
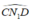là góc nội tiếp chắn nửa đường tròn đường kính CD hay
N
1
,
nằm trên đường tròn đường kính CD
Tương tự như vậy ta chứng minh được N 2 , N 3 nằm trên đường tròn đường kính CD
Vậy N 1 , N 2 , N 3 nằm trên đường tròn đường kính CD