Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

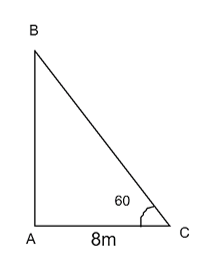
tanˆBCA=ABAC=AB8⇒tan600=AB8⇒AB=8√3(m)≈13,86mtan���^=����=��8⇒tan600=��8⇒��=83(�)≈13,86�
Vậy cây cổ thụ có chiều cao khoảng 13,86 m.

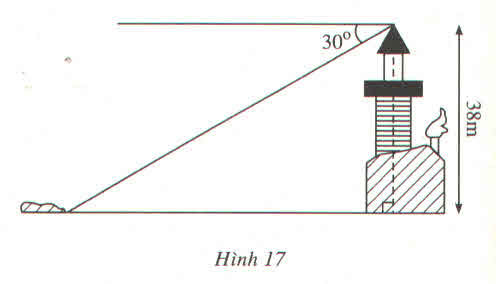
Khoảng cách từ đảo đến chân đèn là:
\(38\cdot\cot30^0\simeq65,818\left(cm\right)\)

Tham khảo:
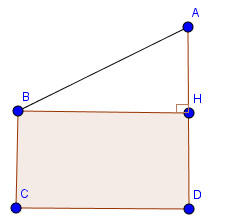
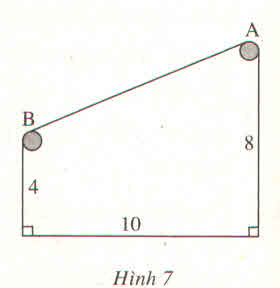
Kẻ BH⊥AD ta được tứ giác BCDH là hình chữ nhật.
Ta có: BC = DH và BH = CD (tính chất hình chữ nhật)
Suy ra: DH = 4 (m)


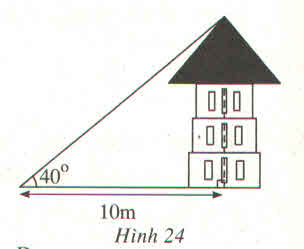
a. Chiều cao tòa nhà là cạnh góc vuông đối diện với góc 40o, khoảng cách từ chỗ người trinh sát đứng đến ngôi nhà là cạnh kề.
Chiều cao của tòa nhà là:
10.tg40o ≈ 8,391 (m)
b. Nếu dịch chuyển sao cho góc “nâng” là 35o thì anh ta cách tòa nhà:
8,391.cotg35o ≈ 11,934 (m)

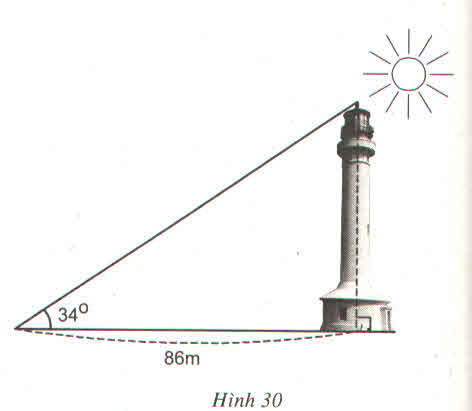
Gọi a là chiều cao của tháp, ta có:
\(\tan34\) = \(\dfrac{c.đối}{c.kề}\)= \(\dfrac{a}{86}\)
\(\Rightarrow a=\) \(\tan34.86\) \(\approx\) 58m
Vậy chiều cao của tháp là 58m

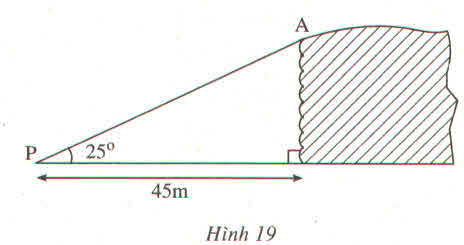
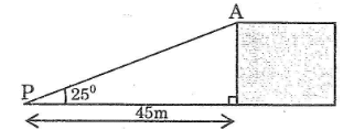
Chiều cao của vách đá là cạnh góc vuông đối diện với góc 25°
Khi đó chiều cao của vách đá là:
45.tg25 ≈ 20,984 (m)
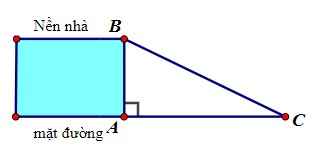
\(tanC=\dfrac{AB}{AC}=\dfrac{4}{7}\Rightarrow C\approx29^045'\)