Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
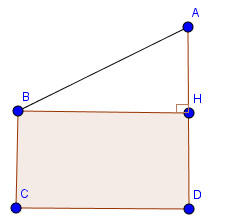
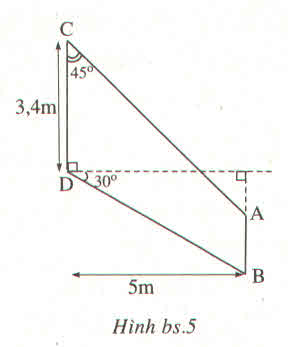
Kẻ BH⊥AD ta được tứ giác BCDH là hình chữ nhật.
Ta có: BC = DH và BH = CD (tính chất hình chữ nhật)
Suy ra: DH = 4 (m)


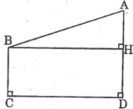
Kẻ BH ⊥ AD ta được tứ giác BCDH là hình chữ nhật.
Ta có: BC = DH và BH = CD (tính chất hình chữ nhật)
Suy ra: DH = 4(cm)
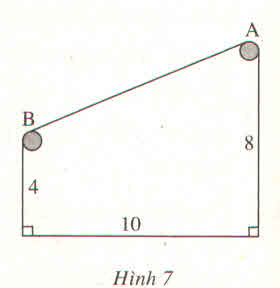
AH = 8 – 4 = 4 (cm)
BH = 10 (cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông ABH, ta có:
A B 2 = B H 2 + A H 2
Suy ra: AB = ![]() ≈ 10,8 (m)
≈ 10,8 (m)
Vậy băng chuyền dài khoảng 10,8 m.

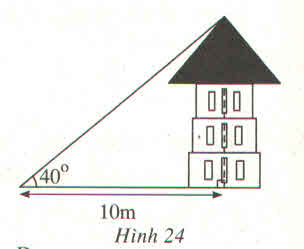
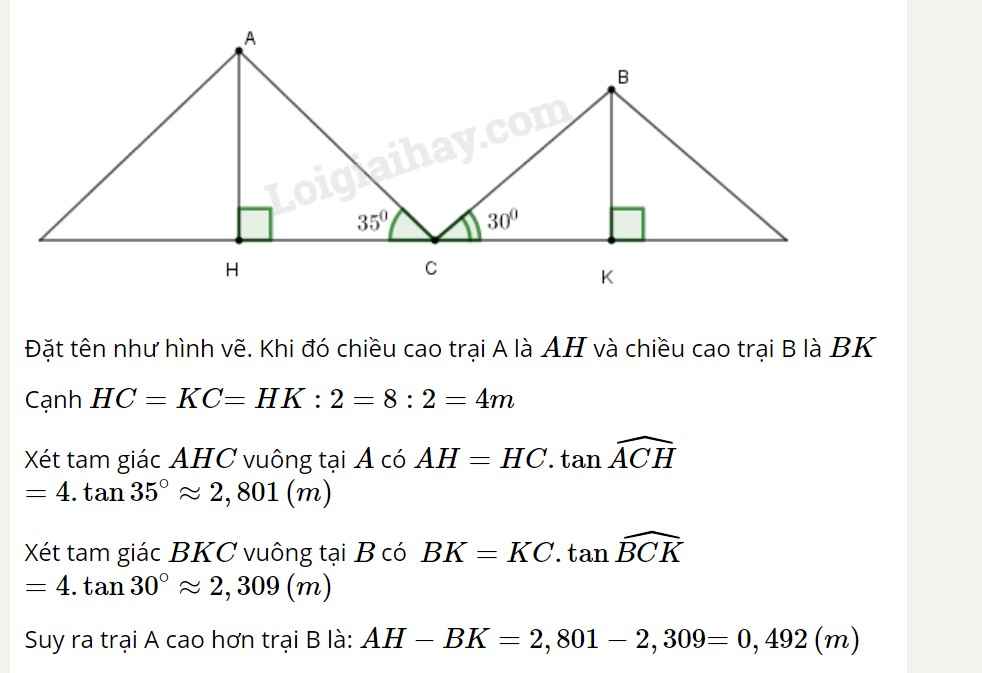
a. Chiều cao tòa nhà là cạnh góc vuông đối diện với góc 40o, khoảng cách từ chỗ người trinh sát đứng đến ngôi nhà là cạnh kề.
Chiều cao của tòa nhà là:
10.tg40o ≈ 8,391 (m)
b. Nếu dịch chuyển sao cho góc “nâng” là 35o thì anh ta cách tòa nhà:
8,391.cotg35o ≈ 11,934 (m)

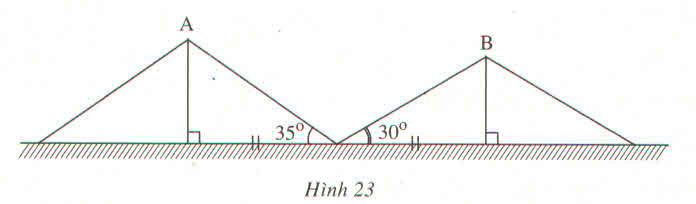
Gọi C là vị trí của máy bay.
Kẻ CH⊥ABCH⊥AB
Trong tam giác vuông ACH, ta có:
AH=CH.cotgˆA(1)AH=CH.cotgA^(1)
Trong tam giác vuông BCH, ta có:
BH=CH.cotgˆB(2)BH=CH.cotgB^(2)
Từ (1) và (2) suy ra:
(AH+BH)=CH.cotgˆA+CH.cotgˆB(AH+BH)=CH.cotgA^+CH.cotgB^
Suy ra:
CH=ABcotgˆA+cotgˆB=ABcotg40∘+cotg30∘≈102,606(cm)

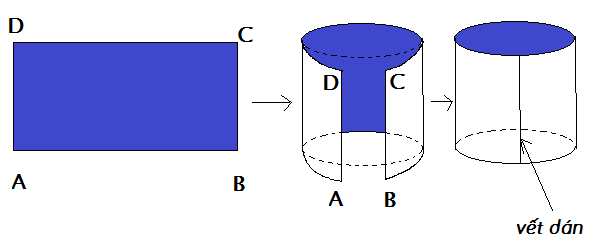
Băng giấy sẽ tạo nên một hình trụ.
Chiều cao của hình trụ là BC = 4cm.
Chú ý: Hình trụ được tạo nên con thiếu hai mặt đáy hình tròn.

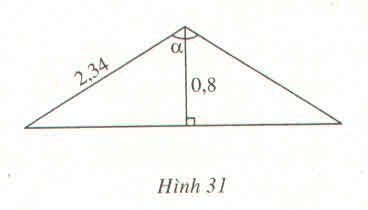
\(cos\dfrac{\alpha}{2}=\dfrac{0,8}{2,34}\Rightarrow\dfrac{\alpha}{2}\approx70^0\Rightarrow\alpha\approx140^0\)
bn gì đó ơi....chỉ rõ cho mk cái chỗ mà cos\(\dfrac{a}{2}=\dfrac{0,8}{2,34}\Rightarrow\dfrac{a}{2}\approx70\)đc hông z......
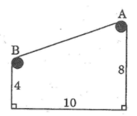


10 4 4 4 A H B 10
\(AB^2=AH^2+HB^2=10^2+4^2=116\)
\(AB=\sqrt{116}\)