

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đường thẳng AC cắt đường thẳng vuông góc với CD tại D ở điểm H thì tam giác CDH là tam giác vuông cân, DH = CD = 3,4m. Đường thẳng AB cắt DH tại K thì DK = 5m nên H nằm giữa D, K (xem h.bs.17).
Dựng hình chữ nhật AKDI thì AIC là tam giác vuông cân, AI = KD = 5m và AC = AI 2 = 5 2 (m).
Trong tam giác vuông BKD, có
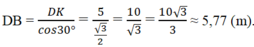
Ta có HKA là tam giác vuông cân, AK = HK = DK – DH = DK – DC = 5 – 3,4 = 1,6.
Ta có KB = DK.tg 30 ° = 5/ 3 = (5 3 )/3, nên suy ra
AB = KB – KA ≈ 1,29 (m).

Gọi C là vị trí của máy bay.
Kẻ CH⊥ABCH⊥AB
Trong tam giác vuông ACH, ta có:
AH=CH.cotgˆA(1)AH=CH.cotgA^(1)
Trong tam giác vuông BCH, ta có:
BH=CH.cotgˆB(2)BH=CH.cotgB^(2)
Từ (1) và (2) suy ra:
(AH+BH)=CH.cotgˆA+CH.cotgˆB(AH+BH)=CH.cotgA^+CH.cotgB^
Suy ra:
CH=ABcotgˆA+cotgˆB=ABcotg40∘+cotg30∘≈102,606(cm)

Tham khảo:
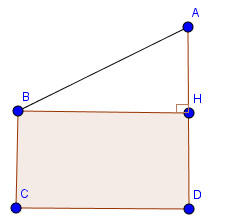
Kẻ BH⊥AD ta được tứ giác BCDH là hình chữ nhật.
Ta có: BC = DH và BH = CD (tính chất hình chữ nhật)
Suy ra: DH = 4 (m)
