



Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.






b: XétΔADE vuông tại E có \(AE=AD\cdot\cos A\)
nên AE=5,16(cm)
AB=AE-BE=2,66(cm)

Xét ΔANB vuông tại N có
\(AN=AB\cdot\sin B\)
nên \(AN\simeq6,772\left(cm\right)\)
XétΔACN vuông tại N có
\(AC=\dfrac{AN}{\sin C}=13,544\left(cm\right)\)

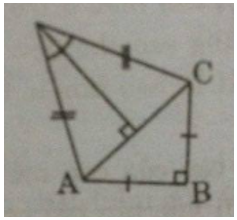
a) Nối AC và kẻ DH⊥ACDH⊥AC
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
AC2=AB2+BC2=122+122=144+144=288AC2=AB2+BC2=122+122=144+144=288
Suy ra: AC=12√2(cm)AC=122(cm)
Ta có: tam giác ACD cân tại D
DH⊥ACDH⊥AC
Suy ra: HA=HC=AC2=6√2(cm)HA=HC=AC2=62(cm)
ˆADH=12ˆADC=20∘ADH^=12ADC^=20∘
Trong tam giác vuông ADH, ta có:
AD=AHsinˆADH=6√2sin20∘≈24,809(cm)AD=AHsinADH^=62sin20∘≈24,809(cm)
b) Ta có:
SABC=12.AB.BC=12.12.12=72SABC=12.AB.BC=12.12.12=72 (cm2)
Trong tam giác vuông ADH, ta có:
DH=AH.cotgˆADH=6√2.cotg20∘≈23,313(cm)DH=AH.cotgADH^=62.cotg20∘≈23,313(cm)
Mặt khác:
SADC=12.DH.AC≈12.23,313.12√2=197,817SADC=12.DH.AC≈12.23,313.122=197,817 (cm2)
Vậy Sdiều =SABC+SADC=72+197,817=269,817=SABC+SADC=72+197,817=269,817 (cm2)
a, nối AC rồi kẻ
Áp dụng định lý Pi-ta-go vào tam giác vuông ABC:
Suy ra:
ta có:tam giác ABC cân tại D
Suy ra:
Trong tam giác vuông ADH, ta có
b, Ta có:
(cm2)
Trong tam giác vuông ADH, ta có:
Mặt khác
(cm2)
Vậy S (cm2)

Kẻ QS⊥PR
Ta có : \(\widehat{QTS}=180^0-\widehat{QTP}=180^0-150^0=30^0\)
Trong tam giác vuông QST, ta có:
\(QS=QT.sinQTS=8.sin30^0=4\left(cm\right)\)
\(TS=QT.cosQTS=8.cos30^0\sim6,928\left(cm\right)\)
Trong tam giác vuông QSP, ta có:
\(SP=QS.cotQPS=4.cot18^0=12,311\left(cm\right)\)
\(PT=SP-TS\sim12,311-6,928\sim5,383\left(cm\right)\)
b) Ta có:
\(S_{QPR}=\frac{1}{2}.QS.PR=\frac{1}{2}.QS.\left(PT+TR\right)\sim\frac{1}{2}.4.\left(5,383+5\right)\sim20,766\left(cm^2\right)\)

Khoảng cách từ đảo đến chân đèn là:
\(38\cdot\cot30^0\simeq65,818\left(cm\right)\)

Chiều cao của vách đá là cạnh góc vuông đối diện với góc 25°
Khi đó chiều cao của vách đá là:
45.tg25 ≈ 20,984 (m)