Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Sơ đồ tạo ảnh : ABL1⟶A1B1L2⟶A2B2AB⟶L1A1B1⟶L2A2B2
Hệ gồm hai thấu kính L1 và L2 đồng trục có tiêu điểm ảnh chính của (L1) trùng với tiêu điểm vật chính của L2=>a=O1O2=f1+f2L2=>a=O1O2=f1+f2
Chùm tia sáng tới song song: =>d1=∞=>d′1=f1=>d2=a−d′1=f2=>d1=∞=>d1′=f1=>d2=a−d1′=f2
=>d′2=∞=>d2′=∞
=> chùm tia ló ra khỏi (L2) cũng là chùm tia song song.
b) Vẽ đường đi của chùm tia sáng ứng với các trường hợp:
(L1 ) và (L2 ) đều là thấu kính hội tụ: hình 30.1
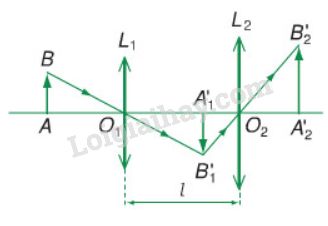
L1 là thấu kính hội tụ; L2 là thấu kính phân kì: Hình 30.2
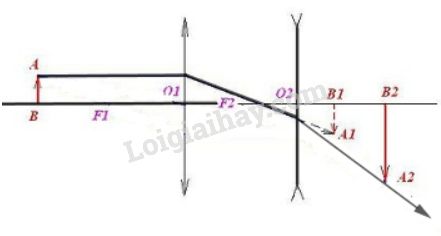
L1 là thấu kính phân kì; L2 là thấu kính hội tụ: Hình 30.3
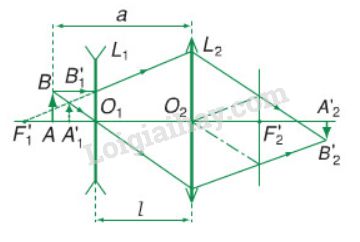

-
-
Ta có:
-
Sơ đồ tạo ảnh:

-
Số bội giác của ảnh ngắm chừng ở vô cực tính theo công thức: G∞=δDf1.f2=80.G∞=δDf1.f2=80.
-
b) * Xét TH quan sát ở điểm cực viễn: (nhắm chừng vô cực) d2'= -OCv= - vô cùng l= f1+f2+ : là độ dài quang học nhá bạn) =>1/f2= 1/d2+ 1/d2' ( vì d2'= - vô cùng) => f2=d2=4 cm =>d1'= l-d2=21-4=17 cm =>d1= (d1'*f1)/(d1'-f1)=1.0625 cm Ta có k=-d1'/d1=-16 =>|k|=16 Ta có: k= A1'B1'/ AB= => A1'B1'= |k|AB tan@= A1'B1'/f2 = |k|AB/f2 (@ là góc trong ảnh đó bạn, cái này áp dụng hệ thức lượng trong tam giác vuông) => AB= tan@*f2/ |k| =>AB= (tan 2' * 4)/ 16=0.0001454 m
-

a) Số bội giác của ảnh: \(G_{\infty}=\dfrac{\delta.OC_C}{f_1.f_2}=\dfrac{16.20}{1.4}=80\)
b) * Xét TH quan sát ở điểm cực viễn: (nhắm chừng vô cực)
d2'= -OCv= - vô cùng
l= f1+f2+ $ =21 cm ($: là độ dài quang học nhá bạn)
=>1/f2= 1/d2+ 1/d2' ( vì d2'= - vô cùng)
=> f2=d2=4 cm
=>d1'= l-d2=21-4=17 cm
=>d1= (d1'*f1)/(d1'-f1)=1.0625 cm
Ta có k=-d1'/d1=-16 =>|k|=16
Ta có: k= A1'B1'/ AB=
=> A1'B1'= |k|AB
tan@= A1'B1'/f2 = |k|AB/f2 (@ là góc trong ảnh đó bạn, cái này áp dụng hệ thức lượng trong tam giác vuông)
=> AB= tan@*f2/ |k|
=>AB= (tan 2' * 4)/ 16=0.0001454 m