Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có \(AB=CD\) (ABCD là hình bình hành)
\(\Rightarrow\frac{AB}{2}=\frac{CD}{2}\)
\(\Rightarrow MB=DN\)(tính chất trung điểm)
Tứ giác BMDN có: \(MB=DN\) (cmt)
MB//DN (AB//CD, ABCD là hình bình hành)
\(\Rightarrow\)Tứ giác BMDN là hình bình hành

a: Xet ΔAHB vuông tại H và ΔAEC vuông tại E có
góc EAC chung
=>ΔAHB đồng dạng với ΔAEC
=>AH/AE=AB/AC
=>AH*AC=AE*AB
b: Xét ΔHCB vuông tại H và ΔFAC vuông tại F có
góc HCB=góc FAC
=>ΔHCB đồng dạng với ΔFAC
=>CH/AF=CB/CA
=>CH*CA=CB*AF=AD*AF
=>AB*AE+AD*AF=AC^2

a. Vì ABCD là HBH => AC và BD cắt nhau tại trung điểm mỗi đường
=> O là trung điểm của AC và BD
=> OA=OC và OB=OD
Xét tam giác AMO và tam giác CNO có:
góc MAO = góc NCO (slt)
OA=OC
góc AOM = góc CON (đối đỉnh)
=> tam giác AMO = tam giác CNO (g-c-g) => MO=NO
b. Ta có: Xét tứ giác DMBN có:
+ 2 đường chéo BD và MN cắt nhau tại O
+ O là trung điểm của MN (do OM=ON) và O là trung điểm của BD
=> DMBN là hBH (Tứ giác có 2 đường chéo cắt nhau tại TĐ mỗi đường là HBH)
vdbruhbhjn tynnmggnfnfbfvjkkm,nmnmj,..,hmn fdbjnkmlikuyjnhgbf vnjkml,o;polikjuynhtgggggybbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb

Ta có :
\(AH^2=AB^2+BH^2\left(1\right)\) (Δ ABH vuông tại H)
\(AH^2=AC^2+CH^2\left(2\right)\) (Δ ACH vuông tại H)
\(\left(1\right),\left(2\right)\Rightarrow AB^2+BH^2=AC^2+CH^2\)
\(\Rightarrow CH^2=AB^2+BH^2-AC^2\)
\(\Rightarrow CH^2=81+676-121=636\)
\(\Rightarrow CH=\sqrt[]{636}=\sqrt[]{4.159}=2\sqrt[]{159}\left(cm\right)\)
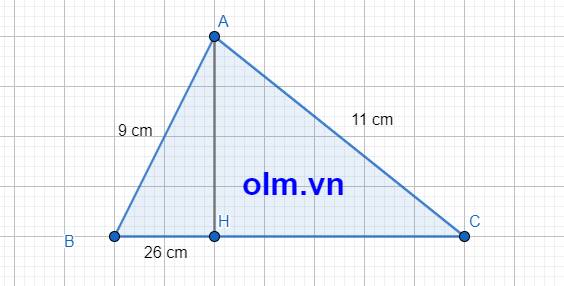
Vì AH là đường cao của tam giác ABC nên AH \(\perp\) BC \(\equiv\) H
⇒ \(\Delta\) AHB \(\perp\) \(\equiv\) H \(\Rightarrow\) AB > BH ⇒ 9 cm > 26 cm vô lý
Em có hai sựa lựa chọn: 1 là em chỉ ra cái sai của cô
2 là em xem lại đề bài của em

Lời giải: