Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Anh đừng buồn bởi đây là những câu hỏi 0.5 đ ở cuối đề thi và có thể mấy bạn học sinh khá hay giỏi mới làm được đó là lớp 9 còn anh lớp 10 thì .... chắc quyên thôi ...

Câu 1:
PT \(\Leftrightarrow\left(x-3\right)\left(x-2\right)=0\) \(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=2\end{matrix}\right.\)
Vậy \(S=\left\{2;3\right\}\)
Câu 2:
a) HPT \(\Leftrightarrow\left\{{}\begin{matrix}2x+4y=10\\3x+4y=5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-5\\y=\dfrac{5-x}{2}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-5\\y=5\end{matrix}\right.\)
Vậy \(\left(x;y\right)=\left(-5;5\right)\)
b) HPT \(\Leftrightarrow\left\{{}\begin{matrix}5x=10\\y=2x-7\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-3\end{matrix}\right.\)
Vậy \(\left(x;y\right)=\left(2;-3\right)\)
Câu 5:
Đặt \(P=\dfrac{1}{x^2+y^2}+\dfrac{1}{xy}=\left(\dfrac{1}{x^2+y^2}+\dfrac{1}{2xy}\right)+\dfrac{1}{2xy}\)
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta có:
\(\dfrac{1}{x^2+y^2}+\dfrac{1}{2xy}\ge\dfrac{4}{x^2+y^2+2xy}=\dfrac{4}{\left(x+y\right)^2}\ge4\)
Áp dụng bất đẳng thức Cosi ta có:
\(2xy\le\dfrac{\left(x+y\right)^2}{2}\le\dfrac{1}{2}\Rightarrow\dfrac{1}{2xy}\ge2\)
\(\Rightarrow P\ge6\)
Dấu "=" xảy ra khi \(x=y=\dfrac{1}{2}\)

5.
Không mất tính tổng quát, giả sử \(c=min\left\{a;b;c\right\}\Rightarrow0\le c\le1\Rightarrow1-\dfrac{c}{2}>0\)
\(P=bc+ca+ab\left(1-\dfrac{c}{2}\right)\ge0\)
\(P_{min}=0\) khi \(\left(a;b;c\right)=\left(0;0;3\right)\) và các hoán vị
\(P=c\left(a+b\right)+ab\left(1-\dfrac{c}{2}\right)\le c\left(3-c\right)+\dfrac{\left(a+b\right)^2}{4}\left(1-\dfrac{c}{2}\right)\)
\(P\le3c-c^2+\dfrac{\left(3-c\right)^2}{4}\left(1-\dfrac{c}{2}\right)\)
\(P\le\dfrac{5}{2}-\dfrac{c^3}{8}+\dfrac{3c}{8}-\dfrac{1}{4}=\dfrac{5}{2}-\dfrac{1}{8}\left(c-1\right)^2\left(c+2\right)\le\dfrac{5}{2}\)
\(P_{max}=\dfrac{5}{2}\) khi \(a=b=c=1\)
Cách 2 phần tìm max bài 5:
Áp dụng BĐT: \(abc\ge\left(a+b-c\right)\left(b+c-a\right)\left(c+a-b\right)\)
\(\Leftrightarrow abc\ge\left(3-2a\right)\left(3-2b\right)\left(3-2c\right)\)
\(\Leftrightarrow abc\ge-8abc+12\left(ab+bc+ca\right)-27\)
\(\Leftrightarrow3abc+27\ge12\left(ab+bc+ca\right)-6abc\)
\(\Leftrightarrow ab+bc+ca-\dfrac{1}{2}abc\le\dfrac{abc}{4}+\dfrac{9}{4}\le\dfrac{1}{4}.\left(\dfrac{a+b+c}{3}\right)^3+\dfrac{9}{4}=\dfrac{5}{2}\)
Dấu "=" xảy ra khi \(a=b=c=1\)

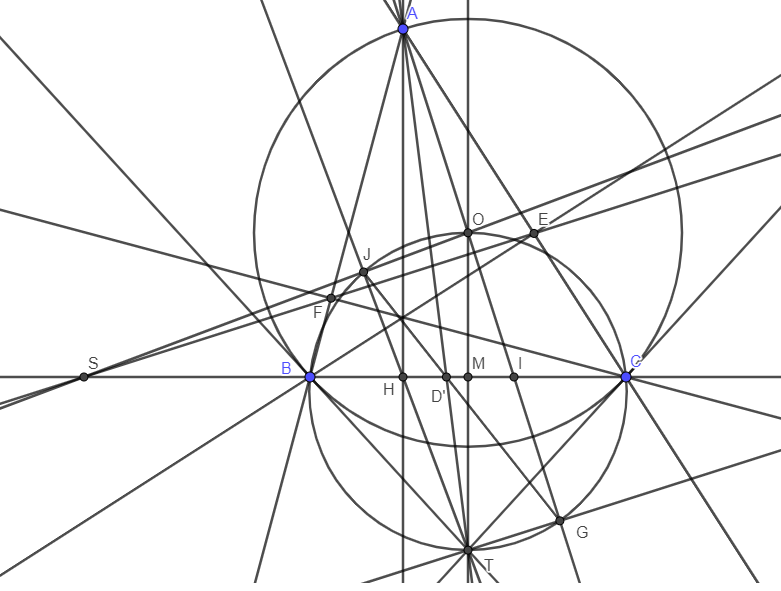
a) Theo phương tích ta có HB . HC = HJ . HT. (1)
Mặt khác do (BCHS) = -1 nên theo hệ thức Maclaurin ta có HB . HC = HM . HS. (2)
Từ (1), (2) suy ra HM . HS = HJ . HT, do đó tứ giác SJMT nội tiếp.
b) Theo hệ thức lượng ta có \(MO.MT=MB^2\).
Mặt khác theo hệ thức Newton, ta có \(MB^2=MH.MS\).
Do đó \(MO.MT=MH.MS\Rightarrow\dfrac{MO}{MS}=\dfrac{MH}{MT}\Rightarrow\Delta MOS\sim\Delta MHT\left(c.g.c\right)\).
Từ đó \(\widehat{MSO}=\widehat{MTH}\Rightarrow SO\perp TH\).
Lại có tứ giác SJMT nội tiếp nên \(\widehat{SJH}=90^o\). Suy ra S, J, O thẳng hàng.
JG cắt BC tại D'. AO cắt BC tại I.
Ta có \(\dfrac{D'B}{D'C}=\dfrac{D'B}{D'J}.\dfrac{D'J}{D'C}=\dfrac{BG}{CJ}.\dfrac{BJ}{CG}=\dfrac{BG}{CG}.\dfrac{BJ}{CJ}\).
Mặt khác do O, T là điểm chính giữa của (BOC) nên JT là phân giác của góc BJC, GO là phân giác của góc BGC. Suy ra \(\dfrac{BG}{CG}=\dfrac{BI}{CI};\dfrac{BJ}{CJ}=\dfrac{BH}{CH}\).
Do đó \(\dfrac{D'B}{D'C}=\dfrac{BG}{CG}.\dfrac{BJ}{CJ}=\dfrac{BI}{CI}.\dfrac{BH}{CH}\).
Lại có AH, AI đẳng giác trong tam giác ABC nên \(\dfrac{BI}{CI}.\dfrac{BH}{CH}=\dfrac{AB^2}{AC^2}\Rightarrow\dfrac{D'B}{D'C}=\dfrac{AB^2}{AC^2}\)
\(\Rightarrow\) AD' là đường đối trung của tam giác ABC.
Mặt khác ta có kết quả quen thuộc AT là đường đối trung của tam giác ABC, do đó \(D'\equiv D\).
Vậy SO, TH, DG đồng quy tại J.

Câu III ý 2)
Ta có:
\(P^2\le\left(a^2+b^2\right)\left[3b\left(a+2b\right)+3a\left(b+2a\right)\right]=2\left[6\left(a^2+b^2\right)+3\cdot2ab\right]\)
\(\le2\left[6\cdot2+3\left(a^2+b^2\right)\right]\le36\Rightarrow P\le6.\)
Đẳng thức xảy ra khi $a=b=1.$
Vậy...
Bài V có phải là 3; 3; 4 không anh Quoc Tran Anh Le CTV?




 .
.
 _
_


























Ngoài ra chúng mình cũng cần tìm thêm nhà tài trợ phụ ngoài nhà tài trợ chính là hoc24.vn ^^ Ai có thể giới thiệu cho chúng mình nhỉ?
đề xuất với ad cho tổ chức cuộc thi thiết kế như cuộc thi thiết kế logo nhé =)))