Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

m = x 2 - 6 x - 7 là phương trình hoành độ giao điểm của đường thẳng y = m và đồ thị (C): y = x 2 - 6 x - 7
Vẽ (P): y = x 2 - 6 x - 7 , lấy đối xứng phần phía dưới Ox của (P) lên trên Ox và xóa đi phần phía dưới Ox (vì y = x 2 - 6 x - 7 , ∀ x ∈ R ), ta được đồ thị (C).
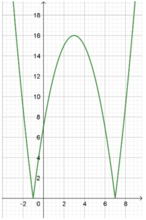
Dựa vào đồ thị: phương trình m = x 2 - 6 x - 7 có 4 nghiệm phân biệt khi m ∈ 0 ; 16 .
Đáp án cần chọn là: B

Điều kiện: - x 2 + 6 x - 9 ≥ 0 ⇔ - x - 3 2 ≥ 0 ⇔ x = 3.
Thử lại ta thấy x = 3 thỏa mãn phương trình.
Vậy phương trình đã cho có nghiệm duy nhất.
Đáp án cần chọn là: B

1.
\(\Leftrightarrow6x^2-12x+7-6\sqrt{6x^2-12x+7}-7=0\)
Đặt \(\sqrt{6x^2-12x+7}=t>0\)
\(\Rightarrow t^2-6t-7=0\Rightarrow\left[{}\begin{matrix}t=-1\left(loại\right)\\t=7\end{matrix}\right.\)
\(\Leftrightarrow\sqrt{6x^2-12x+7}=7\)
\(\Leftrightarrow6x^2-12x+7=49\Rightarrow x=1\pm2\sqrt{2}\)
2.
\(\Delta'=\left(m+1\right)^2-m^2-3=2m-2>0\Rightarrow m>1\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1x_2=m^2+3\end{matrix}\right.\)
\(\left(x_1+x_2\right)^2-2x_1x_2=2x_1x_2+8\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2-8=0\)
\(\Leftrightarrow4\left(m+1\right)^2-4\left(m^2+3\right)-8=0\)
\(\Leftrightarrow2m-4=0\Rightarrow m=2\)

Điều kiện: x 2 - 6 x + 6 ≥ 0 ⇔ x ≤ 3 − 3 x ≥ 3 + 3
Đặt: x 2 − 6 x + 6 = t t ≥ 0
![]()
Khi đó, phương trình trở thành: ⇔ t 2 + 3 = 4 t ⇔ t 2 - 4 t + 3 = 0 ⇔ t = 1 ( t m ) t = 3 ( t m )
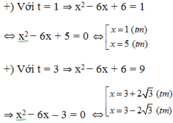
Vậy phương trình có 4 nghiệm.
Đáp án cần chọn là: D

Đáp án C
Ta thấy câu 1), 2) và 4) là các mệnh đề vì ta có thể xét được tính đúng sai của chúng.
Câu 3) không khải mệnh đề vì ta chưa xét được tính đúng sai của nó, chỉ khi cho x một giá trị nào đó thì ta mới nhận được một mệnh đề.
Vậy có 3 mệnh đề.

Đáp án C
Ta thấy câu 1), 2) và 4) là các mệnh đề vì ta có thể xét được tính đúng sai của chúng.
Câu 3) không khải mệnh đề vì ta chưa xét được tính đúng sai của nó, chỉ khi cho x một giá trị nào đó thì ta mới nhận được một mệnh đề.
Vậy có 3 mệnh đề.

Đáp án B.
Ta có:
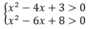
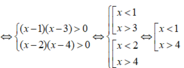
Vậy tập nghiệm của bất phương trình là: ( - ∞ ;1) ∪ (4; + ∞ )

a, \(\left(x-3\right)\left(x^2+x-20\right)\ge0\)
\(\Leftrightarrow\) \(\left(x-3\right)\left(x-4\right)\left(x+5\right)\ge0\)
+) \(x-3=0\Leftrightarrow x=3\); \(x-4=0\Leftrightarrow x=4\); \(x+5=0\Leftrightarrow x=-5\)
+) Lập trục xét dấu f(x) (Bạn tự kẻ trục nha)
\(\Rightarrow\) Bpt có tập nghiệm S = \(\left[-5;3\right]\cup\) [4; \(+\infty\))
b, \(\dfrac{x^2-4x-5}{2x+4}\ge0\)
\(\Leftrightarrow\) \(\dfrac{\left(x-5\right)\left(x+1\right)}{2x+4}\ge0\)
+) \(x-5=0\Leftrightarrow x=5\); \(x+1=0\Leftrightarrow x=-1\); \(2x+4=0\Leftrightarrow x=-2\)
+) Lập trục xét dấu f(x)
\(\Rightarrow\) Bpt có tập nghiệm S = (-2; -1] \(\cup\) [5; \(+\infty\))
c, \(\dfrac{-1}{x^2-6x+8}\le1\)
\(\Leftrightarrow\) \(\dfrac{\left(x-3\right)^2}{\left(x-4\right)\left(x-2\right)}\ge0\)
+) \(x-3=0\Leftrightarrow x=3\); \(x-4=0\Leftrightarrow x=4\); \(x-2=0\Leftrightarrow x=2\)
+) Lập trục xét dấu f(x)
\(\Rightarrow\) Bpt có tập nghiệm S = (\(-\infty\); 2) \(\cup\) (4; \(+\infty\))
Chúc bn học tốt!