Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Quy tắc đặt tương ứng điểm M với điểm M’ nêu trên không phải là một phép biến hình vì M’không phải là điểm duy nhất được xác định trên mặt phẳng
Ví dụ minh họa: a = 4 cm
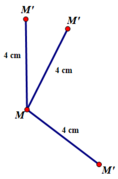

M-> M' => VÊCTỚ MM'= VT u
Tv: M' -> M'' => vt M'M'' = v
áp dụng quy tắc 3 diểm => vt MM' +M'M'' = u+v =w
=> với mỗi điểm M qua phép tt theo vecto w se biến M -> M'' => ĐÓ LÀ PHÉP TT

a) Gọi M' (x₁' ; y₁' ), N' (x₂' ; y₂ )
* M' là ảnh của M qua phép F, nên toạ độ M' thoả:
{x₁' = x₁.cosα – y₁.sinα + a
{y₁' = x₁.sinα + y₁.cosα + b
* N' là ảnh của N qua phép F, nên toạ độ N' thoả:
{x₂' = x₂.cosα – y₂.sinα + a
{y₂' = x₂.sinα + y₂.cosα + b
b) * Khoảng cách d giữa M và N là:
d = MN = √ [(x₂ - x₁)² + (y₂ - y₁)²]
* Khoảng cách d' giữa M' và N' là:
d' = M'N' = √ [(x₂' - x₁' )² + (y₂' - y₁' )²]
= √ {[x₂.cosα – y₂.sinα + a - (x₁.cosα – y₁.sinα + a)]² + [x₂.sinα + y₂.cosα + b - (x₁.sinα + y₁.cosα + b)]²}
= √ {[cosα(x₂ - x₁) - sinα(y₂ - y₁)]² + [sinα(x₂ - x₁) + cosα(y₂ - y₁)]²}
= √ [(x₂ - x₁)².(cos²α + sin²α) + (y₂ - y₁)².(cos²α + sin²α)]
= √ [(x₂ - x₁)² + (y₂ - y₁)²]
c) Phép F là phép dời hình vì: MN = M'N' = √ [(x₂ - x₁)² + (y₂ - y₁)²]
d) Khi α = 0 ⇒ cosα = 1, sinα = 0
Suy ra:
{x' = x + a
{y' = y + b
Đây là biểu thức toạ độ của phép tịnh tiến. Vậy F là phép tịnh tiến

phép dời hình là phép biến điểm thành điểm tia thành tia đoạn thẳng thành đoạn thẳng bằng nó, đừong tròn thành đường tròn cùng bán kính...........(trong sgk định nghĩa ý)
phép dời hình koh làm thay đổi khoảng cách của 2 điểm bất kì
dễ dàng thấy khoảng cách OM và OM' trong phép biến F1 là bằng nhau
con trong phép 2 thì khác nhau nó làm thay đổi khoảng cách nên không là phép biến hình còn nếu muốn tổng quát thì chon điểm n(x1;y1) bất kì rùi so sánh khoảng cách NM và NM'


quy tắc đặt tương ứng mỗi điểm M của mặt phẳng với một điểm xác định duy nhất M’ của mặt phẳng đó gọi là phép biến hình trong mặt phẳng.
chọn đáp án: D