Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{3x^2-12x+12}{x^4-8x}=\frac{3\left(x^2-4x+4\right)}{x\left(x^3-8\right)}=\frac{3\left(x-2\right)^2}{x\left(x-2\right)\left(x^2+2x+4\right)}=\frac{3}{x\left(x^2+2x+4\right)}\)(điều kiện: \(x\ne\left\{0;2\right\}\)
ĐK: \(x\ne\left\{0;2\right\}\)
Ta có: \(3x^2-12x+12\)\(=3\left(x^2-4x+4\right)=3\left(x-2\right)^2\) (1)
\(x^4-8x\)\(=\left(x-2\right)\left(x^3+2x^2+4x\right)\) (chỗ này mình làm hơi tắt xíu,bạn tự giải ra chi tiết nha)
\(=x\left(x-2\right)\left(x^2+2x+4\right)\) (2)
Từ (1) và (2),ta có: \(\frac{3x^2-12x+12}{x^4-8x}=\frac{3\left(x-2\right)^2}{x\left(x-2\right)\left(x^2+2x+4\right)}\)\(=\frac{3\left(x-2\right)}{x\left(x^2+2x+4\right)}\)

a)\(\dfrac{3x^2-12x+12}{x^4-8x}=\dfrac{3\left(x^2-4x+4\right)}{x\left(x^3-8\right)}=\dfrac{3\left(x-2\right)^2}{x\left(x^3-2^3\right)}=\dfrac{3\left(x-2\right)^2}{x\left(x-2\right)\left(x^2+2x+4\right)}=\dfrac{3\left(x-2\right)}{x\left(x^2+2x+4\right)}\)

1) \(\frac{3}{x^2-4y^2}\)
\(=\frac{3}{\left(x-2y\right)\left(x+2y\right)}\)
Phân thức xác định khi \(\left(x-2y\right)\left(x+2y\right)\ne0\)
\(\Rightarrow\hept{\begin{cases}x-2y\ne0\\x+2y\ne0\end{cases}}\Rightarrow x\ne\pm2y\)
2) \(\frac{2x}{8x^3+12x^2+6x+1}\)
\(=\frac{2x}{\left(2x+1\right)^3}\)
Phân thức xác định khi \(\left(2x+1\right)^3\ne0\)
\(\Rightarrow2x+1\ne0\)
\(\Rightarrow x\ne-\frac{1}{2}\)
3) \(\frac{5}{2x-3x^2}\)
\(=\frac{5}{x\left(2-3x\right)}\)
Phân thức xác định khi : \(x\left(2-3x\right)\ne0\)
\(\Rightarrow\hept{\begin{cases}x\ne0\\2-3x\ne0\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x\ne0\\x\ne\frac{2}{3}\end{cases}}\)

a)
+ Phân tích tử số và mẫu số thành nhân tử:
3x2 – 12x + 12 = 3.(x2 – 4x + 4)
= 3.(x2 – 2.x.2 + 22) (Hằng đẳng thức (2))
= 3.(x – 2)2
x4 – 8x = x.(x3 – 8) = x.(x3 – 23) (Hằng đẳng thức (7))
= x.(x – 2)(x2 + x.2 + 22)
= x(x – 2)(x2 + 2x + 4)
+ Rút gọn phân thức:
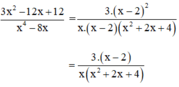
b) + Phân tích tử và mẫu thành nhân tử:
7x2 + 14x + 7 = 7.(x2 + 2x + 1) = 7.(x + 1)2
3x2 + 3x = 3x(x + 1)
+ Rút gọn phân thức
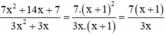


\(a,=\dfrac{\left(x+1\right)\left(x+y\right)}{\left(x-y\right)\left(x+1\right)}=\dfrac{x+y}{x-y}\\ b,=\dfrac{\left(x-3\right)^2}{3x\left(x-3\right)}=\dfrac{x-3}{3x}\\ c,=\dfrac{\left(y-x\right)\left(y+x\right)}{xy\left(x-y\right)}=\dfrac{-x-y}{xy}\)
Lời giải:
a.
\(\frac{x^2+xy+x+y}{x^2-xy+x-y}=\frac{x(x+y)+(x+y)}{x(x+1)-y(x+1)}=\frac{(x+y)(x+1)}{(x+1)(x-y)}=\frac{x+y}{x-y}\)
b.
\(\frac{x^2-6x+9}{3x^2-9x}=\frac{(x-3)^2}{3x(x-3)}=\frac{x-3}{3x}\)
c.
\(\frac{y^2-x^2}{x^2y-xy^2}=\frac{(y-x)(y+x)}{-xy(y-x)}=\frac{x+y}{-xy}\)

Đây là một dạng phân tích thừa số nguyên tố khá quen, cô sẽ hướng dẫn e nhé :) Ta cần ghép các hạng tử để xuất hiện các thành phần chứa biến giống nhau.
\(A=\left(4x+1\right)\left(12x-1\right)\left(3x+2\right)\left(x+1\right)-4=\left(4x+1\right)\left(3x+2\right)\left(12x-1\right)\left(x+1\right)-4\)
\(=\left(12x^2+11x+2\right)\left(12x^2+11x-1\right)-4\)
Đặt \(12x^2+11x+2=t\Rightarrow A=t\left(t-3\right)-4=t^2-3t-4=\left(t-4\right)\left(t+1\right)\)
Quay lại biến x ta có: \(A=\left(12x^2+11x-2\right)\left(12x^2+11x+3\right)\)
Câu sau tương tự nhé :)
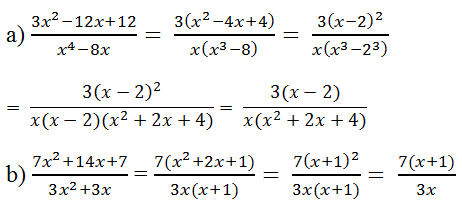
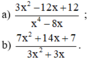

3{x-2}2/x{x-2}{x2+2x+4}=3{x-2}/x2+2x+4=-3/x+2
nho tick minh nha