Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)\(\dfrac{3x^2-12x+12}{x^4-8x}=\dfrac{3\left(x^2-4x+4\right)}{x\left(x^3-8\right)}=\dfrac{3\left(x-2\right)^2}{x\left(x^3-2^3\right)}=\dfrac{3\left(x-2\right)^2}{x\left(x-2\right)\left(x^2+2x+4\right)}=\dfrac{3\left(x-2\right)}{x\left(x^2+2x+4\right)}\)

3{x-2}2/x{x-2}{x2+2x+4}=3{x-2}/x2+2x+4=-3/x+2
nho tick minh nha

Không ai trả lời buồn quá .
\(\frac{3x^2-12x+12}{x^4-8x}\)
\(=\frac{3\left(x^2-4x+4\right)}{x\left(x^3-8\right)}\)
\(=\frac{3\left(x-2\right)^2}{x\left(x-2\right)\left(x^2+2x+2^2\right)}\)
\(=\frac{3\left(x-2\right)}{x\left(x^2+2x+4\right)}\)

1/
x2 - 3x - 4
= \(x^2-3x+\frac{9}{4}-\frac{9}{4}-4\)
\(=\left(x^2-3x+\frac{9}{4}\right)-\frac{25}{4}\)
\(=\left(x-\frac{3}{2}\right)^2-\left(\frac{5}{2}\right)^2\)
\(=\left(x-\frac{3}{2}-\frac{5}{2}\right)\left(x-\frac{3}{2}+\frac{5}{2}\right)\)
\(=\left(x-4\right)\left(x+1\right)\)
Bài 1 :
\(x^2-3x-4\)
\(=x^2+x-4x-4\)
\(=x\left(x+1\right)-4\left(x+1\right)\)
\(=\left(x+1\right)\left(x-4\right)\)

1) \(\left(3x^2-3y^2\right)-\left(12x-12y\right)\)
\(=3xy\left(x-y\right)-12\left(x-y\right)\)
\(=\left(3xy-12\right)\left(x-y\right)\)
2) \(4x^3+4xy^2+8x^2y-16x\)
\(=\left(4x^3-16x\right)+\left(4xy^2+8x^2y\right)\)
\(=4x\left(x^2-4\right)+4xy\left(y+2x\right)\)
Ta có : 3x2 - 3y2 - 12x + 12y
= (3x2 - 3y2) - (12x - 12y)
= 3(x2 - y2) - 12(x - y)
= 3(x - y)(x + y) - 4.3.(x - y)
= 3(x - y)(x + y - 4)

\(x^4+6x^3+12x^2+8x\)
\(=x\left(x^3+6x^2+12x+8\right)\)
\(=x\left(x+2\right)^3\)
8x + 12x2 + 6x3 + x4
= x4 + 6x3 + 12x2 + 8x
= x(x3 + 6x2 + 12x + 8)
= x ( x + 2 ) 3

\(\frac{x^4+x^3-x^2-2x-2}{x^4+2x^3-x^2-4x-2}=\frac{\left(x^4-x^2-2\right)+\left(x^3-2x\right)}{\left(x^4-x^2-2\right)+\left(2x^3-4x\right)}\)
\(=\frac{\left(x^2-2\right)\left(x^2+1\right)+x\left(x^2-2\right)}{\left(x^2-2\right)\left(x^2+1\right)+2x\left(x^2-2\right)}=\frac{\left(x^2-2\right)\left(x^2+x+1\right)}{\left(x^2-2\right)\left(x^2+2x+1\right)}\)
\(=\frac{x^2+x+1}{\left(x+1\right)^2}\)
\(F\left(x\right)=\frac{x^4+x^3-x^2-2x-2}{x^4+2x^3-x^2-4x-2}\)
\(=\frac{\left(x^4+x^3+x^2\right)-2x^2-2x-2}{\left(x^4+2x^3+x^2\right)-\left(2x^2+4x+2\right)}\)
\(=\frac{x^2\left(x^2+x+1\right)-2\left(x^2+x+1\right)}{x^2\left(x^2+2x+1\right)-2\left(x^2+2x+1\right)}=\frac{x^2+x+1}{x^2+2x+1}\)
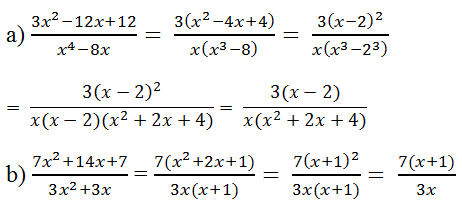

\(\frac{3x^2-12x+12}{x^4-8x}=\frac{3\left(x^2-4x+4\right)}{x\left(x^3-8\right)}=\frac{3\left(x-2\right)^2}{x\left(x-2\right)\left(x^2+2x+4\right)}=\frac{3}{x\left(x^2+2x+4\right)}\)(điều kiện: \(x\ne\left\{0;2\right\}\)
ĐK: \(x\ne\left\{0;2\right\}\)
Ta có: \(3x^2-12x+12\)\(=3\left(x^2-4x+4\right)=3\left(x-2\right)^2\) (1)
\(x^4-8x\)\(=\left(x-2\right)\left(x^3+2x^2+4x\right)\) (chỗ này mình làm hơi tắt xíu,bạn tự giải ra chi tiết nha)
\(=x\left(x-2\right)\left(x^2+2x+4\right)\) (2)
Từ (1) và (2),ta có: \(\frac{3x^2-12x+12}{x^4-8x}=\frac{3\left(x-2\right)^2}{x\left(x-2\right)\left(x^2+2x+4\right)}\)\(=\frac{3\left(x-2\right)}{x\left(x^2+2x+4\right)}\)