Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a,\(x\sqrt{y}+y\sqrt{x}=\sqrt{x}\sqrt{y}.\left(\sqrt{x}+\sqrt{y}\right).\)
c,\(\sqrt{a}-a^2=\sqrt{a}.\left(1-a\sqrt{a}\right)\)
d,\(x-5\sqrt{x}+6=x-3\sqrt{x}-2\sqrt{x}+6\)
\(=\sqrt{x}.\left(\sqrt{x}-3\right)-2.\left(\sqrt{x}-3\right)\)\(=\left(\sqrt{x}-3\right).\left(\sqrt{x}-2\right)\)

a, \(5+\sqrt{5}=\sqrt{5}\left(\sqrt{5}+1\right)\)
b, \(a-2\sqrt{a}=\sqrt{a}\left(\sqrt{a}-2\right)\)
c, \(x-\sqrt{xy}=\sqrt{x}\left(\sqrt{x}-\sqrt{y}\right)\)
d, \(x-y-\sqrt{x}-\sqrt{y}\)
\(=\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)-\left(\sqrt{x}+\sqrt{y}\right)\)
\(=\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}-\sqrt{y}-1\right)\)

a) 2a−4b=2(a−2b)2a−4b=2(a−2b)
c) 2ax−2ay+2a=2a(x−y+1)2ax−2ay+2a=2a(x−y+1)
e) 3xy(x−4)−9x(4−x)=3x(x−4)(y+3)3xy(x−4)−9x(4−x)=3x(x−4)(y+3)
b,d xem lại đề

\(a)\) \(xy-y\sqrt{x}+\sqrt{x}-1\)
= \(y\sqrt{x}.(\sqrt{x}-1)+\sqrt{x}-1\)
=\((\sqrt{x}-1).(y\sqrt{x}+1)\).
\(b)\)\(\sqrt{ax}-\sqrt{by}+\sqrt{bx}-\sqrt{ay}\)
=\(\sqrt{a}.\sqrt{x}-\sqrt{b}.\sqrt{y}+\sqrt{b}.\sqrt{x}-\sqrt{a}.\sqrt{y}\)
=\(\sqrt{a}.\sqrt{x}+\sqrt{b}.\sqrt{x}-\sqrt{a}.\sqrt{y}-\sqrt{b}.\sqrt{y}\)
=\(\sqrt{x}.(\sqrt{a}+\sqrt{b})-\sqrt{y}.(\sqrt{a}+\sqrt{b})\)
=\((\sqrt{x}-\sqrt{y}).(\sqrt{a}+\sqrt{b})\).
\(c)\)\(\sqrt{a+b}+\sqrt{a^2-b^2}\)
=\(\sqrt{a+b}+\sqrt{(a+b).(a-b)}\)
=\(\sqrt{a+b}+\sqrt{a+b}.\sqrt{a-b}\)
=\(\sqrt{a+b}.\left(1+\sqrt{a-b}\right)\).
\(d)\) \(12-\sqrt{x}-x\)
=\(12-4\sqrt{x}+3\sqrt{x}-x\)
=\(4.\left(3-\sqrt{x}\right)+\sqrt{x}\left(3-\sqrt{x}\right)\)
=\(\left(3-\sqrt{x}\right).\left(4+\sqrt{3}\right)\).

\(A,ĐKXĐ:x;y\ge0\)
\(A=\sqrt{xy}-2\sqrt{y}-5\sqrt{x}+10\)
\(=\sqrt{y}\left(\sqrt{x}-2\right)-5\left(\sqrt{x}-2\right)\)
\(=\left(\sqrt{x}-2\right)\left(\sqrt{y}-5\right)\)
\(ĐKXĐ:x;y\ge0\)
\(B=a\sqrt{x}+b\sqrt{y}-\sqrt{xy}-ab\)
\(=\left(a\sqrt{x}-\sqrt{xy}\right)+\left(b\sqrt{y}-ab\right)\)
\(=\sqrt{x}\left(a-\sqrt{y}\right)+b\left(\sqrt{y}-a\right)\)
\(=\sqrt{x}\left(a-\sqrt{y}\right)-b\left(a-\sqrt{y}\right)\)
\(=\sqrt{x}\left(a-\sqrt{y}\right)-b\left(a-\sqrt{y}\right)\)
\(=\left(a-\sqrt{y}\right)\left(\sqrt{x}-b\right)\)

a) \(=9x-9\sqrt{xy}+4\sqrt{xy}-4y\)
\(=\left(9x-9\sqrt{xy}\right)+\left(4\sqrt{xy}-4y\right)\)
\(=9\sqrt{x}\left(\sqrt{x}-\sqrt{y}\right)+4\sqrt{y}\left(\sqrt{x}-\sqrt{y}\right)\)
\(=\left(\sqrt{x}-\sqrt{y}\right)\left(9\sqrt{x}+4\sqrt{y}\right)\)
b)\(=\left(xy+\sqrt{x}.y\right)+\left(\sqrt{x}+1\right)\)
\(=\sqrt{x}y\left(\sqrt{x}+1\right)+\left(\sqrt{x}+1\right)\)
\(=\left(\sqrt{x}+1\right)\left(\sqrt{x}.y+1\right)\)
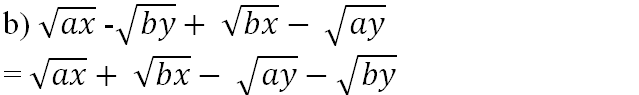
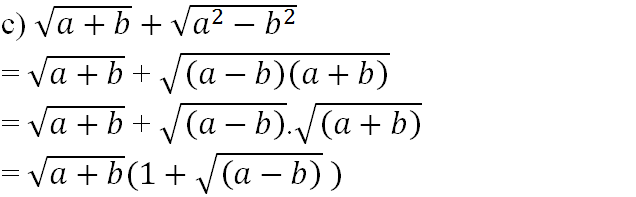
a)
Đa thức bậc nhất không phân tích được nhân tử :v
b)
Đặt \(\sqrt{x}=a;\sqrt{y}=b\) Khi đó:
\(x\sqrt{x}+y\sqrt{y}=a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)\)
c)
Tương tự câu b) thì ta sẽ có:
\(x\sqrt{x}-27=a^3-27=\left(a-3\right)\left(a^2+3a+9\right)\)
Bài làm:
a) \(9x-5=\left(3\sqrt{x}\right)^2-\sqrt{5}==\left(3\sqrt{x}-\sqrt{5}\right)\left(3\sqrt{x}+\sqrt{5}\right)\)
b) \(x\sqrt{x}+y\sqrt{y}=\left(\sqrt{x}\right)^3+\left(\sqrt{y}\right)^3=\left(\sqrt{x}+\sqrt{y}\right)\left(x-\sqrt{xy}+y\right)\)
c) \(x\sqrt{x}-27=\left(\sqrt{x}\right)^3-3^3=\left(\sqrt{x}-3\right)\left(x+3\sqrt{x}+9\right)\)