KL
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PH
2
BM
30 tháng 7 2018
Ta có: \(x^2+2xy+y^2-9z^2=\) \(\left(x+y\right)^2-\left(3z\right)^2\)
\(=\left(x+y-3z\right)\left(x+y+3z\right)\)
23 tháng 9 2017
a) x3-2x2-x+2
=x(x2-1)+2(-x2+1)
=x(x2-1)-2(x2-1)
=(x2-1)(x-2)
b)
x2+6x-y2+9
=x2+6x+9-y2
=(x+3)2-y2
=(x+3-y)(x+3+y)
KH
1
NH
3 tháng 1 2023
a)
\(2x^2y-8xy^2\\ =2xy\left(x-4y\right)\)
b)
\(x^2-2xy+y^2-16\\ =\left(x^2-2xy+y^2\right)-16\\ =\left(x-y\right)^2-16\\ =\left(x-y-4\right)\left(x-y+4\right)\)
PT
1
BT
1
12 tháng 9 2015
a)x^2-4xy+4y^2-4
=(x2-4xy+4y2)-4
=(x-2y)2-4
=(x-2y+2)(x-2y-2)
b)16-x^2+2xy-y^2
=16-(x2-2xy+y2)
=16-(x-y)2
=[4-(x-y)][4+(x-y)]
=(4-x+y)(4+x-y)
13 tháng 2 2018
\(2xy-x^2-y^2+16\)
\(=-\left(x^2-2xy+y^2-16\right)\)
\(=-\left[\left(x^2-2xy+y^2\right)-4^2\right]\)
\(=-\left[\left(x-y\right)^2-4^2\right]\)
\(=-\left[\left(x-y-4\right)\left(x-y+4\right)\right]\)
\(=-\left(x-y-4\right)\left(x-y+4\right)\)
TT
1
24 tháng 9 2016
\(=16-\left(x^2-2xy+y^2\right)\)
\(=4^2-\left(x-y\right)^2=\left(4-x+y\right)\left(4+x-y\right)\)
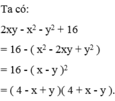
\(x^2-2xy+y^2-16\)
\(=\left(x-y\right)^2-16\)
\(=\left(x-y-4\right)\left(x-y+4\right)\)
p/s: chúc bạn học tốt
\(x^2-2xy+y^2-16\)
\(\Rightarrow\left(x-y\right)^2-16\)
\(\Rightarrow\left(x-y-4\right)\left(x-y+4\right)\)
Code : Breacker