
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn B.
Độ dài của cung 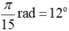 trên đường tròn được tính bằng công thức:
trên đường tròn được tính bằng công thức:
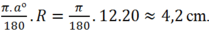

a) Công thức tính diện tích S của bồn hoa là: \(S = \pi .{R^2} = \pi .0,{8^2}\left( {{m^2}} \right)\)
b) Giá trị \(\left| {S - 1,984} \right|\) biểu diễn độ lệch giữa số “1,984” và S.

Gọi bàn kính hình tròn nhỏ là a
=> Bán kính hình tròn lớn là 2a
Ta có
Diện tích hình tròn nhỏ là
\(a^2.3,14\)
Diện tích hình tròn lớn là
\(\left(3a\right)^2.3,14=9a^2.3,14\)
Dễ thấy \(\frac{9a^2.3,14}{a^2.3,14}=9\)
=> Diện tích hình tròn lớn gấp 9 lần diên tích hình tròn nhỏ

a) Dạng chuẩn của số π với 10 chữ số chắc là 3,141592654 với sai số tuyệt đối ∆π≤ 10-9.
b) Viết π ≈ 3,14 ta mắc phải sai số tuyệt đối không quá 0,002. Trong cách viết này có 3 chữ số đáng tin.
Viết π ≈ 3,1416 ta mắc phải sai số tuyệt đối không quá 10-4. Viết như vậy thì số π này có 5 chữ số đáng tin.

Để phương trình x 2 + y 2 + m − 4 x + m + 2 y + 3 m + 10 = là phương trình của một đường tròn có bán kính R = 2 thì:
m − 4 2 2 + m + 2 2 2 − ( 3 m + 10 ) = 2 2 = 4 ⇔ m 2 − 8 m + 16 4 + m 2 + 4 m + 4 4 − 3 m − 10 − 4 = 0 ⇔ 2 m 2 − 4 m + 20 4 − 3 m − 14 = 0
⇔ 2 m 2 − 4 m + 20 − 12 m − 56 = 0 ⇔ 2 m 2 − 16 m − 36 = 0 ⇔ m = 4 ± 34
ĐÁP ÁN A

a) Vì công thức chu vi đường tròn là \(2\pi R\) với R là độ dài bán kính, trong đó \(\pi \) là số không thể tính chính xác được mà chỉ có thể lấy số gần đúng nên hai giá trị tính được là số gần đúng.
b)
Kết quả của An: \({S_1} = 2\pi R \approx 2.3,14.2 = 12,56\) cm:
Kết quả của Bình: \({S_2} = 2\pi R \approx 2.3,1.2 = 12,4\)cm.
Ta thấy \(\pi > 3,14 > 3,1 => 2.\pi. R > {S_1} > {S_2}\)
\( = > \left| {2\pi R - {S_1}} \right| < \left| {2\pi R - {S_2}} \right|\)
Nói cách khác, sai số tuyệt đối của \(S_1\) nhỏ hơn \(S_2\).
=> Kết quả của An chính xác hơn.
Chu vi đường tròn là:
\(P = 2\pi R = 2\pi .1 = 2\pi \left( {cm} \right)\)
Bấm máy tính ta thấy \(2\pi \approx 6,28\)
Vậy \(P \approx 6,28cm\).
Chú ý
Ta có thể lấy số gần đúng khác của \(2\pi \) như: 6,283 hoặc 6,283185