Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Bán kính hình tròn B gấp 3 lần bán kính hình tròn A thì chu vi hình trong B gấp 3 lần chu vi hình tròn A
Do đó nếu hình A quay quanh B thì nó phải quay 3 vòng để trở lại điểm xuất phát

Cách 1: Quãng đường mà hình tròn A lăn được bằng quãng đường di chuyển của tâm hình tròn A. Tâm I của hình tròn A cách tâm hình tròn B một khoảng bằng 4 lần bán kính của hình tròn A (tương ứng, chu vi của đường tròn mà I vạch nên cũng gấp 4 lần chu vi hình A). Vì vậy, hình A phải thực hiện 4 vòng quay mới trở lại điểm xuất phát.
Cách 2: Dễ thấy chu vi hình B gấp 3 lần chu vi hình A. Chia đường tròn lớn thành 3 phần bằng nhau bởi 3 điểm M, N, P (hình vẽ), mỗi phần như vậy có độ dài bằng chu vi hình A. Khi hình A lăn từ M đến N theo chiều kim đồng hồ, bán kính nối tâm hình tròn A với điểm tiếp xúc giữa 2 hình tròn (bán kính màu đen) quét một góc 3600+1200. Tương tự cho 2 phần còn lại, để hình A trở về điểm xuất phát thì bán kính màu đen quét 1 góc tổng cộng là: 3 x ( 3600 + 1200 ) = 4 x 3600, tức 4 vòng quay.

Ta thấy: Bán kính hình trong B gấp 3 lần bán kính hình tròn A
=> Chu vi hình B gấp 3 lần chu vi hình A. Ta chia đường tròn lớn thành 3 phần bằng nhau bởi 3 điểm M, N, P ; mỗi phần như vậy có độ dài bằng chu vi hình A. Khi hình A lăn từ M đến N theo chiều kim đồng hồ, bán kính nối tâm hình tròn A với điểm tiếp xúc giữa 2 hình tròn (bán kính màu đen) quét một góc 3600+1200.. Tương tự cho 2 phần còn lại, để hình A trở về điểm xuất phát thì bán kính màu đen quét 1 góc tổng cộng là 3x(3600+1200)=4x3600, tức 4 vòng quay.

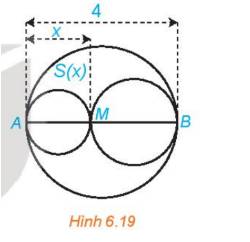
Ta có: AM<AB nên \(0 < x < 4\)
Diện tích hình tròn đường kính AB là \({S_0} = \pi .{\left( {\frac{{AB}}{2}} \right)^2} = 4\pi \)
Diện tích hình tròn đường kính AM là \({S_1} = \pi .{\left( {\frac{{AM}}{2}} \right)^2} = \frac{{\pi .{x^2}}}{4}\)
Diện tích hình tròn đường kính MB là \({S_2} = \pi .{\left( {\frac{{MB}}{2}} \right)^2} = \pi .\frac{{{{\left( {4 - x} \right)}^2}}}{4}\)
Diện tích phần hình phẳng nằm trong hình tròn lớn và nằm ngoài hai hình tròn nhỏ là \(S(x) = {S_0} - {S_1} - {S_2} = 4\pi - \frac{{{x^2}}}{4}\pi - \frac{{{{\left( {4 - x} \right)}^2}}}{4}\pi = \frac{{ - {x^2} + 4x}}{2}\pi \)
Vì diện tich S(x) không vượt quá 1 nửa tổng diện tích hai hình tròn nhỏ nên:
\(S(x) \le \frac{1}{2}\left( {{S_1} + {S_2}} \right)\)
Khi đó : \(\frac{{ - {x^2} + 4x}}{2}\pi \le \frac{1}{2}.\frac{{{x^2} - 4x + 8}}{2}\pi \)
\( \Leftrightarrow - {x^2} + 4x \le \frac{{{x^2} - 4x + 8}}{2}\)
\( \Leftrightarrow - 2{x^2} + 8x \le {x^2} - 4x + 8\)
\( \Leftrightarrow 3{x^2} - 12x + 8 \ge 0\)
Xét tam thức \(3{x^2} - 12x + 8\) có \(\Delta ' = 12 > 0\) nên f(x) có 2 nghiệm phân biệt \({x_1} = \frac{{6 - 2\sqrt 3 }}{3};{x_2} = \frac{{6 + 2\sqrt 3 }}{3}\)
Mặt khác a=3>0, do đó ta có bảng xét dấu:
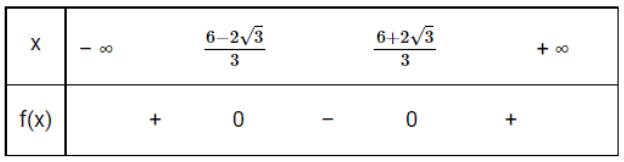
Do đó \(f(x) \ge 0\) với mọi \(x \in \left( { - \infty ;\frac{{6 - 2\sqrt 3 }}{3}} \right] \cup \left[ {\frac{{6 + 2\sqrt 3 }}{3}; + \infty } \right)\)
Mà 0<x<4 nên \(x \in \left( { - \infty ;\frac{{6 - 2\sqrt 3 }}{3}} \right] \cup \left[ {\frac{{6 + 2\sqrt 3 }}{3}; + \infty } \right)\)

a) Diện tích một phần tư hình tròn là: \(\frac{1}{4}\pi {r^2}\)
Gọi x là biến số thể hiện kích thước của bán kính.
Công thức hàm số tính diện tích bồn hoa là: \(f(x) = \frac{1}{4}\pi {x^2}\)
+) Vì bán kính bồn hoa có kích thước từ 0,5 m đến 3 m nên \(0,5 \le x \le 3\)
Vậy tập xác định của hàm số này là \(D = [0,5;3]\)
b) Diện tích là \(0,5\pi \;{m^2}\) tức là\(f(x) = 0,5\pi \;\)
\( \Leftrightarrow \frac{1}{4}\pi {x^2} = 0,5\pi \Leftrightarrow {x^2} = 2 \Rightarrow x = \sqrt 2 \) (do \(0,5 \le x \le 3\))
Vậy bán kính bồn hoa bằng \(\sqrt 2 \;m\).

Do bán kính hình tròn B gấp 3 lần bán kính hình tròn A, nên chu vi của hình tròn B cũng gấp 3 lần chu vi của hình tròn A.
Mà mỗi khi lăn đc 1 vòng, hình tròn A lại đi được một quãng đường bằng đúng chu vi của nó.
Vậy để lăn xung quanh hình B, A phải thực hiện 3 vòng quay để quay lại điểm xuất phát.

a) Công thức tính diện tích S của bồn hoa là: \(S = \pi .{R^2} = \pi .0,{8^2}\left( {{m^2}} \right)\)
b) Giá trị \(\left| {S - 1,984} \right|\) biểu diễn độ lệch giữa số “1,984” và S.

Gọi bàn kính hình tròn nhỏ là a
=> Bán kính hình tròn lớn là 2a
Ta có
Diện tích hình tròn nhỏ là
\(a^2.3,14\)
Diện tích hình tròn lớn là
\(\left(3a\right)^2.3,14=9a^2.3,14\)
Dễ thấy \(\frac{9a^2.3,14}{a^2.3,14}=9\)
=> Diện tích hình tròn lớn gấp 9 lần diên tích hình tròn nhỏ