Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có: \(\frac{323232}{333333}=\frac{32}{33}\)
\(\frac{33333333}{34343434}=\frac{33}{34}\)
ta so sánh : \(\frac{32}{33}< \frac{33}{34}\)
=> \(\frac{323232}{333333}< \frac{33333333}{34343434}\)

a) ta có :
\(\frac{2}{-7}=\frac{-2}{7}=\frac{-22}{77}\) ; \(\frac{-3}{11}=\frac{-21}{77}\)
vì \(\frac{-22}{77}<\frac{-21}{77}\) và 77 > 0 nên \(\frac{-22}{77}<\frac{-21}{77}\) hoặc \(\frac{2}{-7}<\frac{-3}{11}\) vậy x < y
b) ta có :
\(\frac{-213}{300}=\frac{-71}{100}\) ; \(\frac{-18}{25}=\frac{-72}{100}\)
vì \(\frac{-71}{100}>\frac{-72}{100}\) nên \(\frac{-213}{300}>\frac{18}{-25}\) vậy x > y
c) ta có - 0,75 = \(\frac{-75}{100}=\frac{-3}{4}\) vậy x = y

a) \(\frac{2}{3a}-\frac{3}{a}=\frac{2}{3a}-\frac{9}{3a}=\frac{-7}{3a}=\frac{7}{15}\Leftrightarrow-3a=15\Leftrightarrow a=-5\)
b)\(2x^3-1=15\Leftrightarrow2x^3=16\Leftrightarrow x^3=8\Leftrightarrow x=2\)
\(\Rightarrow\frac{2+16}{9}=\frac{y-15}{16}=2\Leftrightarrow y-15=32\Leftrightarrow y=47\)
c) \(\left|x\right|=3\Rightarrow\orbr{\begin{cases}x=-3\\x=3\end{cases}}\) rồi xét 2 trường hợp để tính A nhé :)
Bài 1: ĐK của a: \(a\ne0\)
Quy đồng VT ta có: \(\frac{2a-9a}{3a^2}=\frac{7}{15}\)
\(\Leftrightarrow\frac{-7a}{3a^2}=\frac{7}{15}\)
\(\Leftrightarrow-7a.15=3a^2.7\)
\(\Leftrightarrow-105a=21a^2\)
\(\Leftrightarrow-105a-21a^2=0\)
\(\Leftrightarrow a\left(-105-21a\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}a=0\left(l\right)\\-105-21a=0\end{cases}\Leftrightarrow a=-5\left(n\right)}\)
Vậy:..

a)Áp dụng t/c dãy tỉ số bằng nhau ta có:
x/3=y/5=x+y/3+5=16/8=2
x/3=2 =>x=2x3=6
y/5=2 =>y=2x5=10
Vậy x=6;y=10
b)Áp dụng t/c dãy tỉ số bằng nhau ta có:
x/2=y/(-5)=x-y/2-(-5)=(-7)/7=-1
x/2=-1 =>x=-1x2=-2
y/(-5)=-1 => y=-1x-5=5
Vậy x=-2;y=5

Câu 1:
\(x^4=16\)
\(\Rightarrow x=2\) hoặc \(x=-2\)
Vậy \(x\in\left\{2;-2\right\}\)
Câu 2:
\(\left(x+5\right)^3=-64\)
\(\Rightarrow\left(x+5\right)^3=\left(-4\right)^3\)
\(\Rightarrow x+5=-4\)
\(\Rightarrow x=-9\)
Vậy \(x=-9\)
Câu 4:
Giải:
Ta có: \(\frac{x}{2}=\frac{y}{-5}\) và \(x-y=-7\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{2}=\frac{y}{-5}=\frac{x-y}{2-\left(-5\right)}=\frac{-7}{7}=-1\)
+) \(\frac{x}{2}=-1\Rightarrow x=-2\)
+) \(\frac{y}{-5}=-1\Rightarrow y=5\)
Vậy cặp số \(\left(x;y\right)\) là \(\left(-2;5\right)\)
Câu 5:
Giải:
Đổi 10km = 10000m
Gọi 10000m dây đồng nặng x ( kg )
Vì số dây đồng tỉ lệ thuận với số cân nặng nên ta có:
\(\frac{5}{43}=\frac{10000}{x}\)
\(\Rightarrow x=\frac{10000.43}{5}=86000\left(kg\right)\)
Vậy 1km dây đồng nặng 86000 kg
Câu 6:
Giải:
Gọi số học sinh giỏi, khá , trung bình của khối 7 là a, b, c \(\left(a;b;c\in N\right)\)
Ta có: \(\frac{a}{2}=\frac{b}{3}=\frac{c}{5}\) và \(c+b-a=180\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{5}=\frac{c+b-a}{3+5-2}=\frac{180}{6}=30\)
+) \(\frac{a}{2}=30\Rightarrow a=60\)
+) \(\frac{b}{3}=30\Rightarrow b=90\)
+) \(\frac{c}{5}=30\Rightarrow c=150\)
Vậy số học sinh giỏi là 60 học sinh
số học sinh khá là 90 học sinh
số học sinh trung bình là 150 học sinh
Câu 7:
a) Ta có: \(y=f\left(x\right)=x^2-8\)
\(f\left(3\right)=3^2-8=9-8=1\)
\(f\left(-2\right)=\left(-2\right)^2-8=4-8=-4\)
b) Khi y = 17
\(\Rightarrow17=x^2-8\)
\(\Rightarrow x^2=25\)
\(\Rightarrow x=5\) hoặc \(x=-5\)
Vậy \(x\in\left\{5;-5\right\}\)
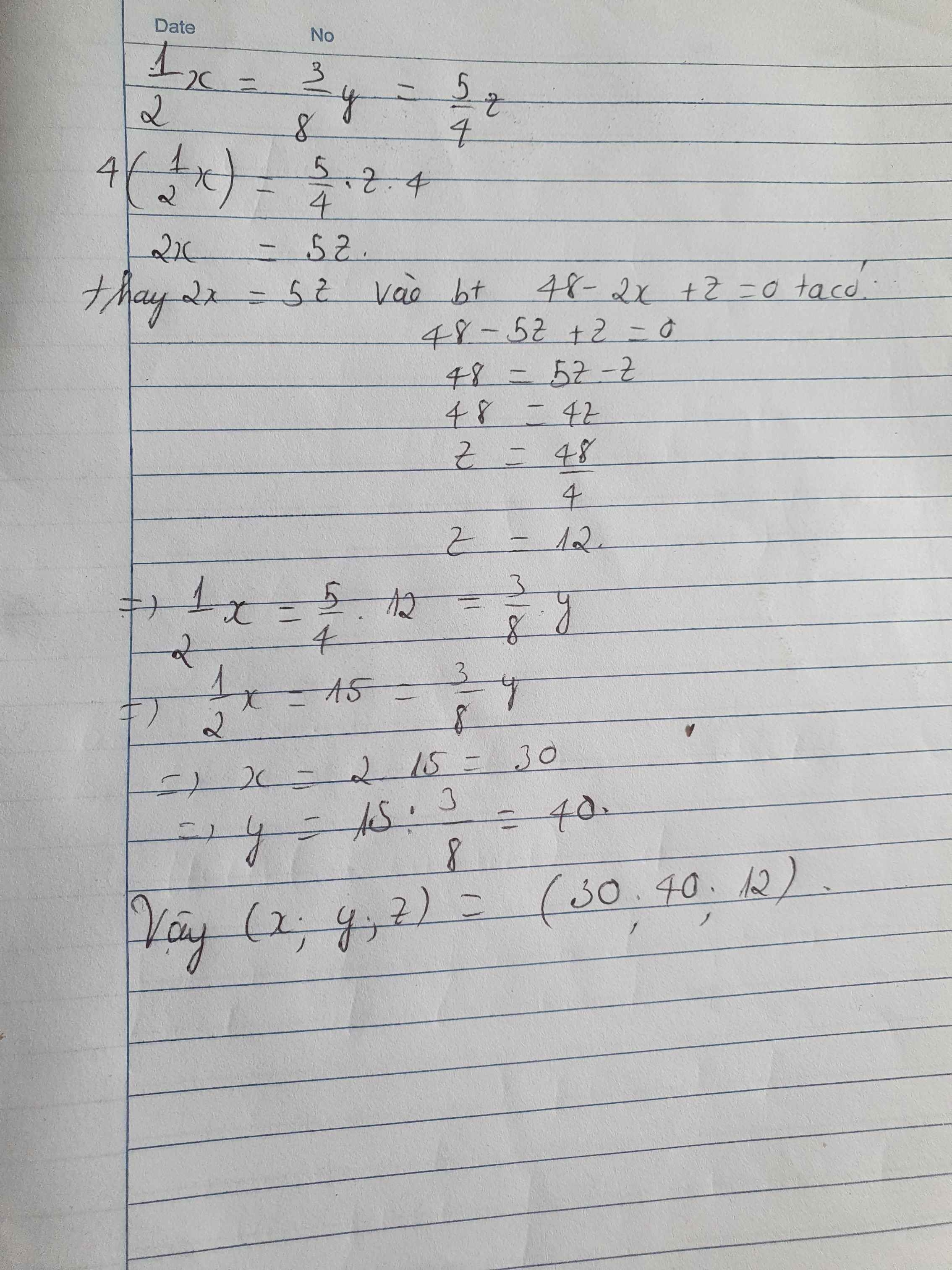
đề bài bạn ơi