Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 7:
(d): \(y=2\left(m+1\right)x-m-1\)
\(\Leftrightarrow y=2mx+2x-m-1\)
=>y=m(2x-1)+2x-1
Tọa độ điểm cố định mà (d) luôn đi qua là:
\(\left\{{}\begin{matrix}2x-1=0\\y=2x-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=0\end{matrix}\right.\)
Bài 8:
y=mx+1
Tọa độ điểm cố định mà (d) luôn đi qua là:
\(\left\{{}\begin{matrix}x=0\\y=m\cdot x+1=m\cdot0+1=1\end{matrix}\right.\)
Bài 9:
Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}5x-3=x+1\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x=4\\y=x+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=1\\y=1+1=2\end{matrix}\right.\)
Thay x=1 và y=2 vào (d3), ta được:
1*m+4=2
=>m+4=2
=>m=-2

a: \(A=\cos^215^0+\cos^225^0+\cos^235^0+...+\cos^255^0+\cos^265^0+\cos^275^0\)
\(=1+1+1+\dfrac{1}{2}\)
\(=\dfrac{7}{2}\)


Theo hd giải => nội suy thế này
Chú đến câu cuối Đến C xe dừng hẳn => V=0 vậy thôi
Tại C vận tốc =0
v= -8t+a
v=0 => -8t +a => t =a/8 (cái a chính là vận tốc thuộc đoạn AB)
Mình chưa hiểu sâu về dạng chuyển động biến đổi
nhưng với bài này cho biểu thức rồi => bản chất lại là toán => Nội suy theo toán học mà làm thôi
còn gì chưa hiểu --> cứ thảo luận


c) A = x.M + (4x + 7)/(√x + 3)
= 3x/(√x + 3) + (4x + 7)/(√x + 3)
= (7x + 7)/(√x + 3)
Để A nhỏ nhất thì 7x + 7 nhỏ nhất
Mà x ≥ 0
⇒ 7x + 7 ≥ 7
⇒ GTNN của A là 7/3 khi x = 0

Lời giải:
Áp dụng định lý Viet đối với pt $x^2+3x-7=0$ ta có:
$x_1+x_2=-3$
$x_1x_2=-7$
Khi đó:
$\frac{1}{x_1-1}+\frac{1}{x_2-1}=\frac{x_2-1+x_1-1}{(x_1-1)(x_2-1)}$
$=\frac{(x_1+x_2)-2}{x_1x_2-(x_1+x_2)+1}=\frac{-3-2}{-7-(-3)+1}=\frac{5}{3}$
$\frac{1}{x_1-1}.\frac{1}{x_2-1}=\frac{1}{(x_1-1)(x_2-1)}=\frac{1}{x_1x_2-(x_1+x_2)+1}=\frac{1}{-7-(-3)+1}=\frac{-1}{3}$
Khi đó áp dụng định lý Viet đảo, $\frac{1}{x_1-1}, \frac{1}{x_2-1}$ là nghiệm của pt:
$x^2-\frac{5}{3}x-\frac{1}{3}=0$
Lời giải:
Áp dụng định lý Viet đối với pt $x^2+3x-7=0$ ta có:
$x_1+x_2=-3$
$x_1x_2=-7$
Khi đó:
$\frac{1}{x_1-1}+\frac{1}{x_2-1}=\frac{x_2-1+x_1-1}{(x_1-1)(x_2-1)}$
$=\frac{(x_1+x_2)-2}{x_1x_2-(x_1+x_2)+1}=\frac{-3-2}{-7-(-3)+1}=\frac{5}{3}$
$\frac{1}{x_1-1}.\frac{1}{x_2-1}=\frac{1}{(x_1-1)(x_2-1)}=\frac{1}{x_1x_2-(x_1+x_2)+1}=\frac{1}{-7-(-3)+1}=\frac{-1}{3}$
Khi đó áp dụng định lý Viet đảo, $\frac{1}{x_1-1}, \frac{1}{x_2-1}$ là nghiệm của pt:
$x^2-\frac{5}{3}x-\frac{1}{3}=0$


 giải giúp mình ạ mình ko hiểu cách làm lắm
giải giúp mình ạ mình ko hiểu cách làm lắm

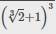 mn giải chi tiết giúp mình bước tách ra được ko ạ tại mình ko hiểu cách tách lắm. cảm ơn mn !
mn giải chi tiết giúp mình bước tách ra được ko ạ tại mình ko hiểu cách tách lắm. cảm ơn mn !
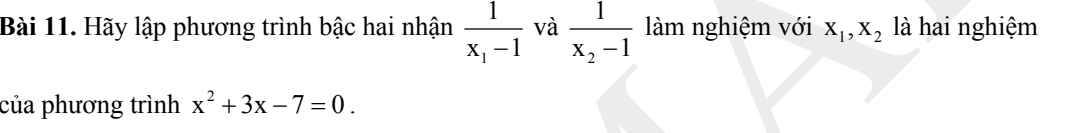

Câu c của em đấy nhé: \(\sqrt{-4x+5}\) có nghĩa ⇔ -4\(x\) + 5 ≥ 0
4\(x\) ≤ 5
\(x\) ≤ \(\dfrac{5}{4}\)
Vậy em kéo dấu ≤ vào ô trống thứ nhất, sau đó em kéo \(\dfrac{5}{4}\) vào ô trống thứ hai rồi ấn nút nộp bài là xong em nhé