Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để làm bài này bạn cần áp dụng 1 số kết quả sau:
+ \(\omega=\omega_1\) thì \(u_{Cmax}\) \(\Rightarrow Z_C^2=Z^2+Z_L^2\) (*)
+ \(\omega = \omega_2\) thì \(u_{Lmax}\), khi đó hệ số công suất của mạch trong 2 trường hợp là như nhau.
Do vậy, ta tìm hệ số công suất của mạch trong trường hợp \(\omega=\omega_1\)
Ta có: \(U_C=3U\Rightarrow Z_C=3Z\)
(*) \(\Rightarrow (3Z)^2=Z^2+Z_L^2\)\(\Rightarrow Z_L=2\sqrt 2Z\)
Có: \(Z^2=R^2+(Z_L-Z_C)^2\) \(\Rightarrow Z^2=R^2+(2\sqrt 2 Z-3Z)^2\)
\(\Rightarrow Z^2=(17-12\sqrt 2)Z^2+R^2\)
\(\Rightarrow R=\sqrt{12\sqrt2 -16}.Z\)
\(\Rightarrow \cos\varphi=\dfrac{R}{Z}=\sqrt{12\sqrt2 -16}\)

Hai giá trị của tần số góc cho cùng một giá trị của U C thõa mãn ω C 1 2 + ω C 2 2 = 2 ω C 2
Đáp án A

Đáp án B
+ Hai giá trị của tần số góc cho cùng dòng điện hiệu dụng trong mạch thỏa mãn
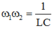

Câu hoàn toàn tương tự như câu hỏi này mình đã trả lời ở đây, bạn tham khảo nhé:
/hoi-dap/question/15708.html

khi w=wo trong mạch xảy ra cộng hưởng ,cường độ dòng điện hiêu dụng là I max,còn khi w=w1 hoặc w=w2 thì dòng điện trong mạch có cùng giá trị hiệu dụng
nên \(\omega_0^2=\omega_1\omega_2=\frac{1}{LC}\Rightarrow\omega_2L=\frac{1}{\omega_1C}\Rightarrow Z_{L2}=Z_{C1}\)
\(I_{max}=\frac{U}{R}\)
\(I=\frac{U}{\sqrt{R^2+\left(Z_{L1}-Z_{C1}\right)^2}}=\frac{U}{\sqrt{R^2+\left(Z_{L1}-Z_{L2}\right)^2}}\)
Theo giả thiết: \(I=\frac{I_{max}}{\sqrt{5}}\)
\(\Rightarrow\frac{U}{\sqrt{R^2+\left(Z_{L1}-Z_{L2}\right)^2}}=\frac{U}{\sqrt{5}R}\Rightarrow R^2+\left(Z_{L1}-Z_{L2}\right)^2=5R^2\)
\(\Rightarrow\left|Z_{L1}-Z_{L2}\right|=2R\)
\(\Rightarrow L\left(\omega_2-\omega_1\right)=2R\Rightarrow\frac{1}{\pi}.150\pi=2R\Rightarrow R=75\Omega\)
Đáp án B.

Viết biểu thức UAN
\(U_{AN}=I.Z_{AN}=\frac{U\sqrt{R^2+Z_L^2}}{\sqrt{R^2+\left(Z_L-Z_C\right)^2}}\)
Ta thấy khi \(Z_L=\left|Z_L-Z_C\right|\) thì \(U_{AN}=U\)
Khi đó UAN không phụ thuộc vào R.
\(\Rightarrow Z_L=Z_C-Z_L\Leftrightarrow Z_C=2Z_L\)
\(\Leftrightarrow\frac{1}{\omega C}=2\omega L\)\(\Leftrightarrow\omega=\frac{1}{\sqrt{2LC}}=\omega_1\)

\(I_1 = I_2\)
<=> \(\frac{U_1}{\sqrt{R^2 + (Z_{L1}-Z_{C1})^2}} = \frac{U_2}{\sqrt{R^2 + (Z_{L2}-Z_{C2})^2}}\)
<=> \((Z_{L1} -Z_{C1})^2 = (Z_{L2} -Z_{C2})^2 \) (do \(U_1 = U_2=U= const\))
<=> \(\omega_1L - \frac{1}{\omega_1C} = \omega_2L - \frac{1}{\omega_2C} => \omega_1 = \omega_2\) (loại)
hoặc \(\omega_1L - \frac{1}{\omega_1C} =- \omega_2L + \frac{1}{\omega_2C}\)=> \(L(\omega_1+ \omega_2) = \frac{1}{C} \frac{\omega_1+\omega_2}{\omega_1\omega_2}\)
=> \(\omega_1\omega_2 = \frac{1}{LC}.\)
Chọn đáp án.A.\(\omega_1\omega_2 = \frac{1}{LC}\)