Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hai giá trị của tần số góc cho cùng một giá trị của U C thõa mãn ω C 1 2 + ω C 2 2 = 2 ω C 2
Đáp án A

Bạn áp dụng kết quả này của bài toán mạch RLC có C thay đổi để Uc max:
umạch vuông pha với uRL
Ta có giản đồ véc tơ sau:
U U U RL C m i 120 120√3 φ φ
Từ giản đồ véc tơ: \(U_{RL}=\sqrt{3.120^2-120^2}=120\sqrt 2(V)\)
Suy ra hệ số công suất: \(\cos\varphi=\dfrac{U_{RL}}{U_C}=\dfrac{120\sqrt 2}{120\sqrt 3}=\sqrt{\dfrac{2}{3}}\)

Đáp án B
Phương pháp: Điều kiện cực trị khi tần số thay đổi.
Cách giải: Khi tần số góc thay đổi thì có các giá trị để điện áp trên cuộn cảm hay tụ đạt cực đại.
Ta có:
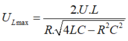
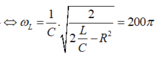
Và điện áp trên tụ cực đại là:
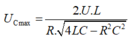
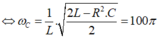
Dễ thấy:
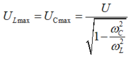
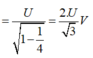

Đáp án B
+ Với ω = ω 1 thì điện áp hiệu dụng ở hai đầu tụ điện đạt giá trị cực đại
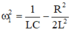
và
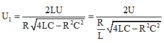
+ Với
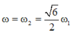
thì điện áp hiệu dụng ở hai đầu điện trở đạt giá trị cực đại
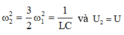
Mặc khác
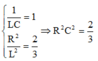
+ Khi
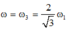
điện áp hiệu dụng trên hai đầu tụ điện là
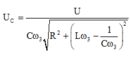
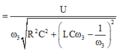
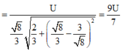
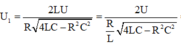
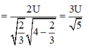
Từ đó ta tìm được
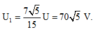

Đáp án B
Phương pháp: điều kiện cực trị khi tần số thay đổi.
Cách giải:
Khi tần số góc thay đổi thì có các giá trị để điện áp trên cuộn cảm hay tụ đạt cực đại. ta có:
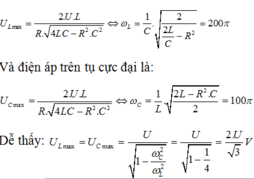

Ta có ω 1 2 = 1 L C
Chuẩn hóa R = 1 Z L = x ⇒ Z C = x
Giả sử rằng tần số góc ω 2 = n ω 1 , khi đó ta có
U A M = U 1 2 + n x 2 1 2 + n x − x n 2 = U 1 + x 2 n 2 − 2 x 2 1 + n x 2
Để U A M không phụ thuộc vào R thì
x 2 n 2 − 2 x 2 = 0 ⇒ x = 0 n = 1 2 ⇒ f 2 = f 1 2
Đáp án D

Hệ số công suất của đoạn mạch khi xảy ra cực đại với điện áp trên tụ hoạc trên cuộn dây cos φ = 2 1 + n
Mặc khác U U L m a x 2 + 1 n 2 = 1 → ω L ω C = 2 3
→ Vậy cos φ = 2 1 + n = 0 , 96
Đáp án D

Hệ số công suất của đoạn mạch khi xảy ra cực đại với điện áp trên tụ hoạc trên cuộn dây cos φ = 2 1 + ω L ω C
Mặc khác U U L m a x 2 + ω C ω L 2 = 1 ⇒ ω C ω L = 3 2
→ Vậy cos φ = 2 1 + ω L ω C = 0 , 96
Đáp án D
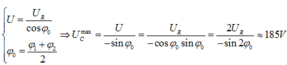
Để làm bài này bạn cần áp dụng 1 số kết quả sau:
+ \(\omega=\omega_1\) thì \(u_{Cmax}\) \(\Rightarrow Z_C^2=Z^2+Z_L^2\) (*)
+ \(\omega = \omega_2\) thì \(u_{Lmax}\), khi đó hệ số công suất của mạch trong 2 trường hợp là như nhau.
Do vậy, ta tìm hệ số công suất của mạch trong trường hợp \(\omega=\omega_1\)
Ta có: \(U_C=3U\Rightarrow Z_C=3Z\)
(*) \(\Rightarrow (3Z)^2=Z^2+Z_L^2\)\(\Rightarrow Z_L=2\sqrt 2Z\)
Có: \(Z^2=R^2+(Z_L-Z_C)^2\) \(\Rightarrow Z^2=R^2+(2\sqrt 2 Z-3Z)^2\)
\(\Rightarrow Z^2=(17-12\sqrt 2)Z^2+R^2\)
\(\Rightarrow R=\sqrt{12\sqrt2 -16}.Z\)
\(\Rightarrow \cos\varphi=\dfrac{R}{Z}=\sqrt{12\sqrt2 -16}\)