Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để cường độ dòng điện trong mạch đạt cực đại thì cần điều chỉnh tần số đến giá trị \(f_0\)
\(\Rightarrow f_0=\sqrt{f_1.f_2}=\sqrt{25.100}=50(hz)\)

Dựa theo biểu thức w để Uc (hoặc UL) max (\(\sqrt{\frac{L}{C}-\frac{R^2}{2}}\) có nghĩa), em có thể dễ dàng chứng mình đc:
Khi tăng dần tốc độ góc ω từ 0 đến ∞ thì điện áp trên các linh kiện sẽ lần lượt đạt cực đại theo thứ tự: C, R, L.

Cường độ dòng điện: \(I=\frac{U}{\sqrt{R^2+\left(Z_L-Z_C\right)^2}}\)
Theo giả thiết ta có: \(\omega_0=\sqrt{\omega_1\omega_2}=\sqrt{60\pi.40\pi}=20\sqrt{6}\pi\)
\(\omega_0=\frac{1}{\sqrt{LC}}\Rightarrow C=\frac{1}{\omega_0^2L}=\frac{1}{20^2.6.\pi^2.\frac{2,5}{\pi}}=\frac{10^{-3}}{6\pi}F\)
\(I_{max}=\frac{U}{R}\)
\(I_1=\frac{I_{max}}{\sqrt{5}}\Rightarrow\frac{U}{Z_1}=\frac{U}{R.\sqrt{5}}\Rightarrow5R^2=R^2+\left(Z_{L1}-Z_{C1}\right)^2\)
\(\Rightarrow R^2=\frac{1}{4}\left(Z_{L1}-Z_{C1}\right)^2\Rightarrow R=\frac{\left|Z_{L1}-Z_{C1}\right|}{2}\)(*)
\(Z_{L1}=60\pi.\frac{2,5}{\pi}=150\Omega\)
\(Z_{C1}=\frac{1}{60\pi.\frac{10^{-3}}{6\pi}}=100\Omega\)
Thay vào (*) ta đc: R = 25 ôm
Đáp án D.

Đáp án B
I = U R 2 + ω L - 1 ω L 2 . Theo bài I 1 = I 2 = I m a x 5 hay Z 1 = Z 2 = 5 Z
R 2 + L ω 1 - 1 C ω 1 2 = R 2 + L ω 2 - 1 C ω 2 2 = 5 R
Kết hợp với ω1 > ω2 → khi ω = ω1 mạch có tính cảm kháng, khi ω = ω2 mạch có tính dung kháng.
L ω 1 - 1 C ω 1 = 2 R L ω 2 - 1 C ω 2 = - 2 R ⇒ L ω 1 2 - ω 2 2 = 2 R ω 1 + ω 2 ⇒ R = L ω 1 - ω 2 2 = 25 Ω

ü Đáp án B
+ Hai giá trị của tần số cho cùng dòng điện hiệu dụng trong mạch là: ![]()
+ Mà
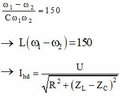

+ Mặc khác:
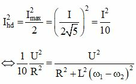
![]()

Đáp án B
+ Hai giá trị của tần số cho cùng dòng điện hiệu dụng trong mạch 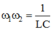 .
.
Ta có 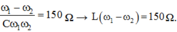
+ Mặc khác
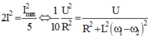 →
→ ![]() .
.
Từ hai phương trình trên ta thu được R = 50 Ω.

Lời giải:
Khi $f=f_1$
$\Rightarrow \sqrt{r^{2}+Z_{L}^{2}}=100$
Mặt khác, khi C biến thiên để $U_{C_{max}}$
$\Rightarrow Z_{C}=\dfrac{r^{2}+Z_{L}^{2}}{Z_{L}}\Leftrightarrow \dfrac{L}{C}=r^{2}+Z_{L}^{2}=100^{2}\left(1\right)$
Khi $f=f_2$
Mạch xảy ra cộng hưởng:
$\Rightarrow LC=\dfrac{1}{\left(200\pi \right)^{2}}\left(2\right)$
Lấy $\left(1\right).\left(2\right)$:
$\Rightarrow L^{2}=\dfrac{1}{4\pi ^{2}}\Rightarrow L=\dfrac{1}{2\pi }\left(H\right)$
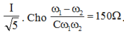 . Giá trị điện trở R trong mạch là
. Giá trị điện trở R trong mạch là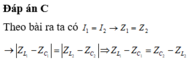
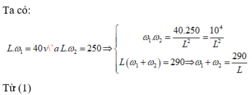
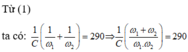
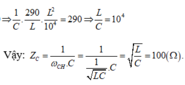
Câu hoàn toàn tương tự như câu hỏi này mình đã trả lời ở đây, bạn tham khảo nhé:
/hoi-dap/question/15708.html
cảm ơn thầy ạ