TL
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NC
0
18 tháng 4 2020
Bài làm
a) Ta có: \(\widehat{OAB}+\widehat{OAP}=180^0\)( hai góc kề bù )
\(\widehat{OBA}+\widehat{MBD}=180^0\)( hai góc kề bù )
Mà \(\widehat{OAB}=\widehat{OBA}\)( Do tam giác OAB cân ở O )
=> \(\widehat{OAP}=\widehat{MBD}\)
Xét tam giác APC và tam giác BMD có:
AC = BD ( gt )
\(\widehat{OAP}=\widehat{MBD}\)( cmt )
PA = MB ( gt )
=> Tam giác APC = tam giác BMD ( c.g.c )
b) Vì tam giác APC = tam giác BMD ( cmt )
=> \(\widehat{DMB}=\widehat{CPA}\)
Mà \(\widehat{BMD}=\widehat{CMA}\)( Hai góc đối )
=> \(\widehat{CMA}=\widehat{CPA}\)
=> Tam giác CMP cân ở C
c) Vì tam giác CMP cân ở C
=> CP = CM ( hai cạnh bên )
Mà CP = MD ( do tam giác APC = tam giác BMD )
=> CM = MD
=> M là trung điểm CD ( đpcm )
TA
2 tháng 1 2018
Xét tam giác OAD và tam giác OBC , có :
Góc O chung
OA = OB ( gt )
OD = OC ( gt )
Suy ra tam giác OAD = tam giác OBC ( c - g - c )
S
2 tháng 1 2018
x O y A C B D K
a, OA = OB; AC = BD => OC = OD
Xét t/g OAD và t/g OBC có:
OA = OB (gt)
góc O chung
OC = OD (cmt)
=> t/g OAD = t/g OBD (c.g.c)
b,Vì t/g OAD = t/gOBD => góc ACK = góc BDK , góc CAK = góc DBK
Xét t/g KAC và t/g KBD có:
góc ACK = góc BDK (cmt)
AC = BD (gt)
góc CAK = góc DBK (cmt)
=> t/g KAC = t/g KBD (g.c.g)
=> AK = BK
Xét t/g OAK và t/g OBK có:
OA = OB (gt)
AK = BK (cmt)
OK chung
=> t/g OAK = t/g OBK (c.c.c)
=> góc AOK = góc BOK
=> OK là tia p/g của góc xOy
CH
Cô Hoàng Huyền
Admin
VIP
5 tháng 3 2018
Em tham khảo tại link dưới đây nhé.
Câu hỏi của Nguyễn Thị Ngọc Ánh - Toán lớp 7 - Học toán với OnlineMath
13 tháng 2 2020
1. a) Vì tam giác ABC cân tại A =>B=ACD Mà ACD=ECN(đối đỉnh) =>B=ECN Vì AB=AC(tam giác ABC cân tại A) Mà AC=IC =>AB=IC Xét tam giác ABD và tam giác ICE có: AB=IC(c/m trên) B=ECN(c/m trên) BD=CE(gt) =>tam giác ABD=tam giác ICE(c.g.c) 2. Xét tam giác BMD và tam giác CEN có: BDM=CNE(=90 độ) BD=CE(gt) B=ECN(c/m trên) =>tam giác BDM=tam giác CEN(g.c.g) =>BM=CN(2 cạnh tương ứng)
NN
14 tháng 4 2020
a) ABC cân tại A (gt) => AB=AC và góc ABC = góc ACB
=> góc ABM = góc ACN ( các góc kề bù với góc ABC và góc ACB)
Xét tam giác ABM và tam giác ACN có
AB=AC
góc ABM= góc ACN (cmt)
BM=CN )gt)
=> tam giác ABM = tam giác ACN ( c.g.c)
=> AM=AN ( 2 cạnh tương ứng)
b) tam giác ABM = tam giác ACN (cmt)
=> góc M= góc N (cặp góc tương ứng)
Xét tam giác HBM và tam giác KCN có
góc BHM= góc CKN =90 độ (BH vuông góc AM, AN vuông góc CK)
BM = CN (Gt)
góc M= góc N (cmt)
=> tam giác HBM = tam giác KCN ( cạnh huyền - góc nhọn)
c) TA có tam giác HBC và tam giác KCN (cmt)
=> góc HBM = góc KCN (hai goc tương ứng)
MÀ góc HBM = góc CBO ( hai góc đối đỉnh )
góc KCN=góc BCO ( hai góc đối đỉnh )
=> góc CBO= góc BCO
=> tam giác OBC cân tại O ( dấu hiệu nhận biết tam giác vuông)
HM
2
AH
Akai Haruma
Giáo viên
10 tháng 12 2023
Lời giải:
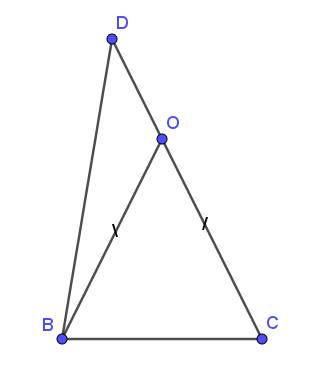
Xét tam giác $OBD$, áp dụng BĐT tam giác thì:
$DB< OB+OD$
Mà $OB=OC$ nên: $OB+OD=OC+OD=CD$
$\Rightarrow DB< CD$ (đpcm)
bạn tự vẽ hình nhé:
xét tam giác AOB có: AB<AO+OB
Do A thuộc tia đối của tia 0C
=>A,O,C thẳng hàng .gọi đây là 1
tg OBC cân tại O.=>OB=OC gọi đây là 2
từ 1 và 2 =>AO+OB=AO+OC=AC
hay AB<AC(dpcm)