Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b) Xét ΔABH vuông tại H và ΔCBA vuông tại A có
\(\widehat{ABH}\) chung
Do đó: ΔABH\(\sim\)ΔCBA(g-g)
Suy ra: \(\dfrac{AB}{CB}=\dfrac{HB}{AB}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AB^2=BC\cdot BH\)(đpcm)
Có gấp thế nào đi nữa thì phải đủ dữ kiện đề tụi tớ mới giúp được cậu nhé :))

a. Xét △ AFC và △ AEB có:
\(\widehat{BAC}\) chung
\(\widehat{AFC}=\widehat{AEB}=90^0\)
⇒ △AFC đồng dạng với △ AEB(g.g)
⇒ \(\frac{AF}{AE}=\frac{AC}{AB}\)
⇒ \(AB.AF=AE.AC\)
\(\frac{AF}{AE}=\frac{AC}{AB}\Rightarrow\frac{AF}{AC}=\frac{AE}{AB}\)
Xét △ AEF và △ ABC có :
\(\widehat{BAC}\) chung
\(\frac{AF}{AC}=\frac{AE}{AB}\left(cmt\right)\)
⇒△ AEF đồng dạng với △ ABC (c.g.c)
Mấy câu kia bạn tự làm nốt đi nhá.

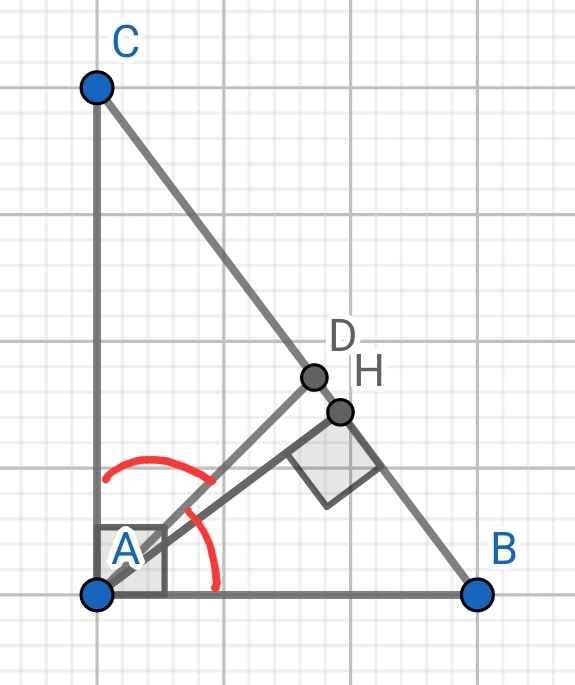
a) Xét hai tam giác vuông: ∆AHB và ∆CHA có:
∠B = ∠CAH (cùng phụ C)
⇒ ∆AHB ∽ ∆CHA (g-g)
⇒ AH/HC = HB/AH
⇒ AH.AH = HB.HC
⇒ AH² = HB.HC
Xét hai tam giác vuông: ∆ABC và ∆HAC có:
∠C chung
⇒ ∆ABC ∽ ∆HAC (g-g)
⇒ AC/HC = BC/AC
⇒ AC.AC = HC.BC
b) ∆ABC vuông tại A
⇒ BC² = AB² + AC² (Pytago)
= 3² + 4²
= 25
⇒ BC = 5 (cm)
Do AD là tia phân giác của ∠BAC
⇒ BD/CD = AB/AC
⇒ AB/BD = AC/CD
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
AB/BD = AC/CD = (AB + AC)/(BD + CD) = (3 + 4)/5 = 7/5
Do AB/BD = 7/5
⇒ BD = AB.5/7 = 3.5/7 = 15/7 (cm)

a) ta có BD là pg => DA/DC=AB/AC=15/10=3/2
=> DA/3=DC/2=DA+DC/3+2=AC/5=15/5=3
=> DA=3.3=9 cm
DC=3.2=6 cm
b) ta có BE là pg ngoài=> EA/EC=AB/BC=15/10=3/2
=> EA/3=EC/2=EA-EC/3-2=AC/1=15/1=15
=> EC=15.2=30cm
a) Áp dụng định lí Pytago vào ΔABC vuông tại A,ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Vậy: BC=10cm
Mấy câu kia thì s