Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi cạnh của tam giác là a, trung điểm BC là I.
+Ta có: \(BC=a\sqrt{2};\text{ }IB=IC=\frac{IA}{2}=\frac{a}{\sqrt{2}}\)
+Ta có: \(MB^2+MC^2=\left(\frac{a}{\sqrt{2}}-IM\right)^2+\left(\frac{a}{\sqrt{2}}+IM\right)^2=a^2+2IM^2\text{ (1)}\)
+AI vừa là trung tuyến vừa là phân giác góc A nên AI là trung trực tam giác ABC.
=> Tam giác AIM vuông tại I
\(\Rightarrow AM^2=AI^2+IM^2=\left(\frac{a}{\sqrt{2}}\right)^2+IM^2=\frac{a^2}{2}+IM^2\)
\(\Rightarrow2AM^2=a^2+2IM^2\text{ (2)}\)
Từ (1) và (2) suy ra \(MB^2+MC^2=2MA^2\)
Gọi cạnh của tam giác là a, trung điểm BC là I.
+Ta có: BC=a√2; IB=IC=IA2 =a√2
+Ta có: MB2+MC2=(a√2 −IM)2+(a√2 +IM)2=a2+2IM2 (1)
+AI vừa là trung tuyến vừa là phân giác góc A nên AI là trung trực tam giác ABC.
=> Tam giác AIM vuông tại I
⇒AM2=AI2+IM2=(a√2 )2+IM2=a22 +IM2
⇒2AM2=a2+2IM2 (2)
Từ (1) và (2) suy ra MB2+MC2=2MA2

Lấy thêm trung điểm K của BC rồi dùng định lý Pytago tính các cạnh MB, MC, MA theo AB, AC, BC, AK
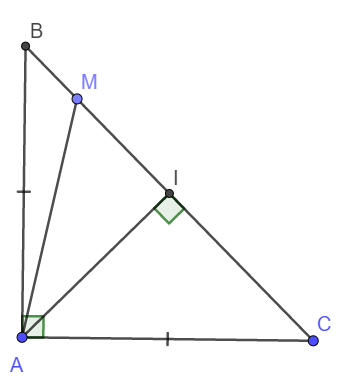
Đặt AB = AC = a \(\Rightarrow BC=\sqrt{AB^2+AC^2}=a\sqrt{2}\)
Gọi I là trung điểm BC, do tam giác ABC cân nên AI cũng là đường cao.
\(AI=BI=IC=\frac{a\sqrt{2}}{2}\)
Đặt MI = x ( 0 < x < \(\frac{a\sqrt{2}}{2}\) )
Ta có \(BM^2=\left(BI-MI\right)^2=\left(\frac{a\sqrt{2}}{2}-x\right)^2\)
\(MC^2=\left(IC+MI\right)^2=\left(\frac{a\sqrt{2}}{2}+x\right)^2\)
\(\Rightarrow MB^2+MC^2=2\left(\frac{a^2}{2}+x^2\right)=2\left(AI^2+MI^2\right)\)
\(=2AM^2\)
Vậy nên ta đã chứng minh được \(\forall M\in BC:BM^2+MC^2=2AM^2\)

hình tự vẽ
a) Tam giác ABC vuông cân tại A
=> góc ABC = góc ACB = 45
Tgiac DBM và tgiac EMC vuông tại D và E có góc DBM = góc ACB = 45
suy ra: tgiac DBM và tgiac EMC vuông cân tại D và E
Áp dụng Pytago ta có:
MB2 = DB2 +DM2
<=> MB2 = 2.DM2
MC2 = EM2 + EC2
<=> MC2 = 2.ME2
suy ra: MB2 + MC2 = 2 . (MD2 + ME2)
Tứ giác ADME có góc A= góc D = góc E = 90 độ
=> ADME là hình chữ nhật
Do đó: MB2 + MC2 = 2.DE2 = 2.MA2 (đpcm)

hình tự vẽ
a) Tam giác ABC vuông cân tại A
=> góc ABC = góc ACB = 45
Tgiac DBM và tgiac EMC vuông tại D và E có góc DBM = góc ACB = 45
suy ra: tgiac DBM và tgiac EMC vuông cân tại D và E
Áp dụng Pytago ta có:
MB2 = DB2 +DM2
<=> MB2 = 2.DM2
MC2 = EM2 + EC2
<=> MC2 = 2.ME2
suy ra: MB2 + MC2 = 2 . (MD2 + ME2)
Tứ giác ADME có góc A= góc D = góc E = 90 độ
=> ADME là hình chữ nhật
Do đó: MB2 + MC2 = 2.DE2 = 2.MA2 (đpcm)

hình tự vẽ
a) Tam giác ABC vuông cân tại A
=> góc ABC = góc ACB = 45
Tgiac DBM và tgiac EMC vuông tại D và E có góc DBM = góc ACB = 45
suy ra: tgiac DBM và tgiac EMC vuông cân tại D và E
Áp dụng Pytago ta có:
MB2 = DB2 +DM2
<=> MB2 = 2.DM2
MC2 = EM2 + EC2
<=> MC2 = 2.ME2
suy ra: MB2 + MC2 = 2 . (MD2 + ME2)
Tứ giác ADME có góc A= góc D = góc E = 90 độ
=> ADME là hình chữ nhật
Do đó: MB2 + MC2 = 2.DE2 = 2.MA2 (đpcm)
