Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Cách 1. Sử dụng các tỉ số lượng giác trong tam giác vuông NAB và NAC chúng ta có BN.tanB = NC.tanC
Chú ý BN + NC = BC chúng ta tính được
BN ≈ 4,67cm => AN ≈ 3,65cm
Cách 2. Gợi ý: Kẻ CH vuông góc với AB tại H
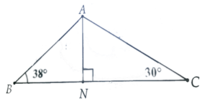
b, Xét ∆ANC vuông có: A C = A N sin C => AC ≈ 7,3cm

kẻ BK vuongAC ^CBK vuong tai K và ^C = 30 độ = > tam giácCBK nửa đều BK = BC/2 = 5,5 ^KBC = 180-(BKA+^C) = 60độ ^KBA = ^KBC-^ABC = 22 độ = >tam giác KBA có KBA = 22 độ = >AB = BK:sinKBA = 5,5:sin22 = 5,93194 AN = AB.sinABN = 3,65207 b) AC = 2AN = 7,30414
38 38 o o A B C K N
Kẻ \(BK\perp AC\left(K\in AC\right)\)
Trong tam giác vuông BKC có:
\(\widehat{KBC}=60^o-30^o=60^o\)
\(\Rightarrow\widehat{KBA}=60^o-38^o=22^o\)
BC = 11 (cm) => BK = 5,5 (cm) ( tính chất cạnh đối diện góc 30° trong tam giác vuông bằng nửa cạnh huyền )
Xét tam giác ABK vuông tại K : \(\cos KBA=\frac{BK}{AB}\)
\(\Rightarrow AB=\frac{BK}{\cos KBA}=\frac{5,5}{\cos22^o}\approx5,93\left(cm\right)\)
Xét tam giác ANB vuông tại N : \(\sin ABN=\frac{AN}{AB}\)
\(\Rightarrow AN=AB\sin ABN=5,93.\sin38^o\approx3,65\left(cm\right)\)
b) Xét tam giác ANC vuông tại N : \(\sin ACN=\frac{AN}{AC}\)
\(AC=\frac{AN}{\sin ACN}\approx\frac{3,65}{\sin30^o}\approx7,3\left(cm\right)\)


c)
K ẻ B N ⊥ A C N ∈ A C . B A C ⏜ = 60 0 ⇒ A B N ⏜ = 30 0 ⇒ A N = A B 2 = c 2 ⇒ B N 2 = A B 2 − A N 2 = 3 c 2 4 ⇒ B C 2 = B N 2 + C N 2 = 3 c 2 4 + b − c 2 2 = b 2 + c 2 − b c ⇒ B C = b 2 + c 2 − b c
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC, R là bán kính đường tròn ngoại tiếp tam giác ABC. Xét tam giác đều BCE có R = O E = 2 3 E M = 2 B C 3 3.2 = 1 3 . 3 b 2 + c 2 − b c

e làm chứng minh dc góc NPI = BAC=60 độ, thế e ghi tương tự vs góc PNI=BAC=60 độ dc k ạ