Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

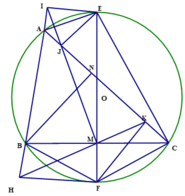
b) Ta có I E M ⏜ = A E C ⏜ ⇒ A E I ⏜ = C E M ⏜ .
Mặt khác A E I ⏜ = A J I ⏜ ( cùng chắn cung IJ), C E M ⏜ = C J M ⏜ ( cùng chắn cung CM). Suy ra C J M ⏜ = A J I ⏜ . Mà I, M nằm hai phía của đường thẳng AC nên C J M ⏜ = A J I ⏜ đối đỉnh suy ra I, J, M thẳng hàng.
Tương tự, ta chứng minh được H, M, K thẳng hàng.
Do tứ giác CFMK nội tiếp nên C F K ⏜ = C M K ⏜ .
Do tứ giác CMJE nội tiếp nên J M E ⏜ = J C E ⏜ .
Mặt khác E C F ⏜ = 90 0 ⇒ C F K ⏜ = J C E ⏜ ( vì cùng phụ với A C F ⏜ ).
Do đó C M K ⏜ = J M E ⏜ ⇒ J M K ⏜ = E M C ⏜ = 90 0 hay I J ⊥ H K

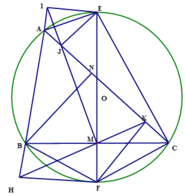
a) Ta có: A I E ^ = A J E ^ = 90 0 nên tứ giác AIEJ nội tiếp.
E M C ^ = E J C ^ = 90 0 nên tứ giác CMJE nội tiếp.
Xét tam giác Δ A E C v à Δ I E M , có
A C E ⏜ = E M I ⏜ ( cùng chắn cung JE của đường tròn ngoại tiếp tứ giác CMJE).
E A C ⏜ = E I M ⏜ ( cùng chắn cung JE của đường tròn ngoại tiếp tứ giác AIEJ).
Do đó hai tam giác Δ A E C ~ Δ I E M đồng dạng
⇒ A E E I = E C E M ⇒ E A . E M = E C . E I (đpcm)

c)
K ẻ B N ⊥ A C N ∈ A C . B A C ⏜ = 60 0 ⇒ A B N ⏜ = 30 0 ⇒ A N = A B 2 = c 2 ⇒ B N 2 = A B 2 − A N 2 = 3 c 2 4 ⇒ B C 2 = B N 2 + C N 2 = 3 c 2 4 + b − c 2 2 = b 2 + c 2 − b c ⇒ B C = b 2 + c 2 − b c
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC, R là bán kính đường tròn ngoại tiếp tam giác ABC. Xét tam giác đều BCE có R = O E = 2 3 E M = 2 B C 3 3.2 = 1 3 . 3 b 2 + c 2 − b c