Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Kẻ BK⊥ACBK⊥AC
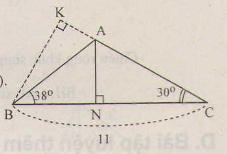
Ta được: ˆKBC=60∘KBC^=60∘ và ˆKBA=60∘=60∘−38∘=22∘KBA^=60∘=60∘−38∘=22∘
Xét tam giác KBC vuông tại K có:
BK=BC⋅sinC=11⋅sin30∘=5,5(cm)BK=BC⋅sinC=11⋅sin30∘=5,5(cm)
Xét tam giác KBA vuông tại K có:
AB=BKcos22∘=5,5cos22∘≈5,932(cm).AB=BKcos22∘=5,5cos22∘≈5,932(cm).
Xét tam giác ABN vuông tại N có:
AN=AB⋅sin38∘≈5,932⋅sin38∘≈3,652(cm)AN=AB⋅sin38∘≈5,932⋅sin38∘≈3,652(cm)
b) Xét tam giác ANC vuông tại N có AC=ANsinC≈

Bài 2:
Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)và\(AH\perp BC\)
\(\Rightarrow AH^2=HB.HC\)(Hệ thức lượng)
\(AH^2=25.64\)
\(AH=\sqrt{1600}=40cm\)
Xét \(\Delta ABH\)có\(\widehat{H}=90^o\)
\(\Rightarrow\tan B=\frac{AH}{BH}\)\(=\frac{40}{25}=\frac{8}{5}\)
\(\Rightarrow\widehat{B}\approx58^o\)
Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)
\(\Rightarrow\widehat{B}+\widehat{C}=90^o\)
\(58^o+\widehat{C}=90^o\)
\(\Rightarrow\widehat{C}\approx90^o-58^o\)
\(\widehat{C}\approx32^o\)

a}ta có C=300 nên sinC=\(\frac{1}{2}\Rightarrow\frac{AB}{BC}=\frac{1}{2}\Rightarrow AB=10.\frac{1}{2}=5\)cm
cosC=\(\frac{\sqrt{3}}{2}\Rightarrow\frac{AC}{BC}=\frac{\sqrt{3}}{2}\Rightarrow AC=10.\frac{\sqrt{3}}{2}=5\sqrt{3}cm\)
b từ H kẻ HN và HM lần lượt với AC, AB là vuông góc đúng ko nếu là vuông góc thì
tứ giác HMAN là hình chữ nhật vì có 3 góc vuông
nên MN =AH
ta có AH.BC=AB.AC
AH=\(\frac{5.5\sqrt{3}}{10}=\frac{5\sqrt{3}}{2}\)=MN
c}ta có B=90-C=600
tam giác vuông ABH có cosB=\(\frac{BH}{AB}\)=>cos60=\(\frac{BH}{5}\)\(\Rightarrow\frac{1}{2}=\frac{BH}{5}\Rightarrow BH=2,5\)
ta có BC.\(cos^2B\)=BC.cos2600=10.\(\left(\frac{1}{2}\right)^2=10.\frac{1}{4}=2.5=BH\)
=> BC.cos2B=BH
nếu tháy đúng thì tick nha

ĐỀ BÀI THIẾU \(\widehat{BAC}=105^0\). Hình vẽ trong TKHĐ

Qua A kẻ đường thẳng vuông góc với AC cắt BC tại M. Tại E kẻ đường thẳng song song với AH cắt AC tại D.
Xét tam giác ABE có AB=BE=1 mà ^ABE=600 nên tam giác ABE đều. Khi đó
\(AH=AB\cdot\sin\widehat{ABH}=\sin60^0=\frac{\sqrt{3}}{2}\)
Dễ thấy \(\Delta MAE=\Delta ADE\left(g.c.g\right)\Rightarrow AD=AM\Rightarrow\Delta\)AMC vuông tại A có đường cao AH theo hệ thức lượng:
\(\frac{1}{AC^2}+\frac{1}{AM^2}=\frac{1}{AH^2}\Rightarrow\frac{1}{AC^2}+\frac{1}{AD^2}=\frac{1}{\left(\frac{\sqrt{3}}{2}\right)^2}=\frac{4}{3}\)

Gọi F đối xứng với C qua A. Khi đó tam giác FBC vuông tại F.
Theo hệ thức lượng thì \(BC^2=HC\cdot CF\). Mặt khác \(BC^2=2AB\cdot HC\)
Đến đây dễ rồi nha, làm tiếp thì chán quá :(

a) Từ A kẻ AE//BD cắt đường thẳng CB tại E
=> ^BAE=^DBA=^B/2=60* và ^ABE=60* (kề bù với ^B)
=> ∆ABE đều nên AB=BE=AE=6
Do BD//AE suy ra: BD/AE=CB/CE
mà CE=CB+BE=12+6=18cm
ta có BD/6=12/18 suy ra BD=12.6/18=4 (cm)
b) Xét ∆ABM có AB=BM =6cm (do BM=MC=BC/2)
nên ∆ABM cân tại B mà BD là đường phân giác nên cũng là đường cao
do đó BD vuông góc với AM.
a) Ta có:
ˆABD=ˆCBD=ˆABC2=120∘2=60∘ABD^=CBD^=ABC^2=120∘2=60∘
Từ A kẻ đường thẳng song song với BD cắt CD tại E.
Lại có:
ˆBAE=ˆABD=60∘BAE^=ABD^=60∘ (so le trong)
ˆCBD=ˆAEB=60∘CBD^=AEB^=60∘ (đồng vị)
Suy ra tam giác ABE đều
⇒AB=BE=EA=6(cm)(1)⇒AB=BE=EA=6(cm)(1)
Khi đó: CE = BC + BE = 12 + 6 = 18 (cm)
Tam giác ACE có AE // BD nên suy ra:
BCCE=BDAE⇒BD=BC.AECE=12.618=4(cm)
b) Ta có:
MB=MC=12.BC=12.12=6(cm)(2)MB=MC=12.BC=12.12=6(cm)(2)
Từ (1) và (2) suy ra:
BM=AB⇒BM=AB⇒ ∆ABM cân tại B.
Tam giác cân ABM có BD là đường phân giác nên đồng thời nó cũng là đường cao (tính chất tam giác cân). Vậy BD⊥AM
a, Cách 1. Sử dụng các tỉ số lượng giác trong tam giác vuông NAB và NAC chúng ta có BN.tanB = NC.tanC
Chú ý BN + NC = BC chúng ta tính được
BN ≈ 4,67cm => AN ≈ 3,65cm
Cách 2. Gợi ý: Kẻ CH vuông góc với AB tại H
b, Xét ∆ANC vuông có: A C = A N sin C => AC ≈ 7,3cm