Bài 5 : Cho \(\Delta ABC\) có AB = AC , lấy M là trung điểm của BC . Trên tia đối của tia BC lấy điểm D , trên tia đối của tia CB lấy điểm E sao cho BD = CE . Chứng minh :b )\(\Delta ABD=\Delta ACE\) a ) AM vuông góc với BC c )\(\Delta ACD=\Delta ABE\) d ) AM là tia phân giác của góc DAEBài 6 : Cho tam giác ABC ( AC > AB ) . Tia phân giác của góc BAC cắt BC tại D. Trên cạnh AC lấy E sao cho AE = AB .a ) Chứng minh BD...
Đọc tiếp
Bài 5 : Cho \(\Delta ABC\) có AB = AC , lấy M là trung điểm của BC . Trên tia đối của tia BC lấy điểm D , trên tia đối của tia CB lấy điểm E sao cho BD = CE . Chứng minh :
b )\(\Delta ABD=\Delta ACE\) a ) AM vuông góc với BC
c )\(\Delta ACD=\Delta ABE\) d ) AM là tia phân giác của góc DAE
Bài 6 : Cho tam giác ABC ( AC > AB ) . Tia phân giác của góc BAC cắt BC tại D. Trên cạnh AC lấy E sao cho AE = AB .
a ) Chứng minh BD = DE
b ) Kéo dài AB và DE cắt nhau tại K. Chứng minh góc AKD bằng góc ACD .
c ) Chứng minh \(\Delta KBE=\Delta CEB\)
d ) Tìm điều kiện của tam giác ABC để DE vuông góc với AC .
Bài 7 Cho tam giác ABC , P là trung điểm của AB . Đường thẳng qua P và song song với BC cắt AC ở đường thẳng qua Q và song song với AB cắt BC ở F. Chứng minh rằng :
a ) AP = QF
b ) \(\Delta APQ=\Delta QFC\)
c ) Q là trung điểm của AC
d ) Lấy điểm I thuộc tia đối của tia QP sao cho QI = QP . Chứng minh CI // AB
Bài 8 : Cho đoạn thẳng AB . Trên hai nửa mặt phẳng đối nhau bờ AB , kẻ tia Ax và By cùng vuông góc với AB . Trên tia Ax , By lần lượt lấy hai điểm C , D sao cho AC = BD .
a ) Chứng minh AD = BC
. b ) Chứng minh AD // BC .
c ) Gọi 0 là trung điểm của AB . Trên BC lấy điểm E , trên AD lấy điểm F sao cho CE = DF . Chứng minh ( là trung điểm của EF .
Mình đang cần gấp ạ



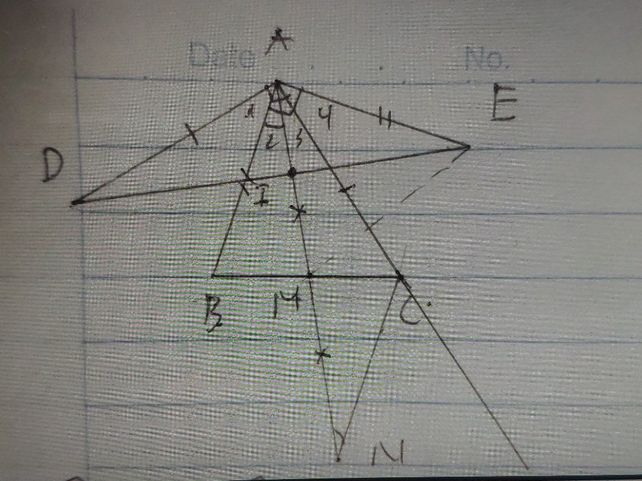

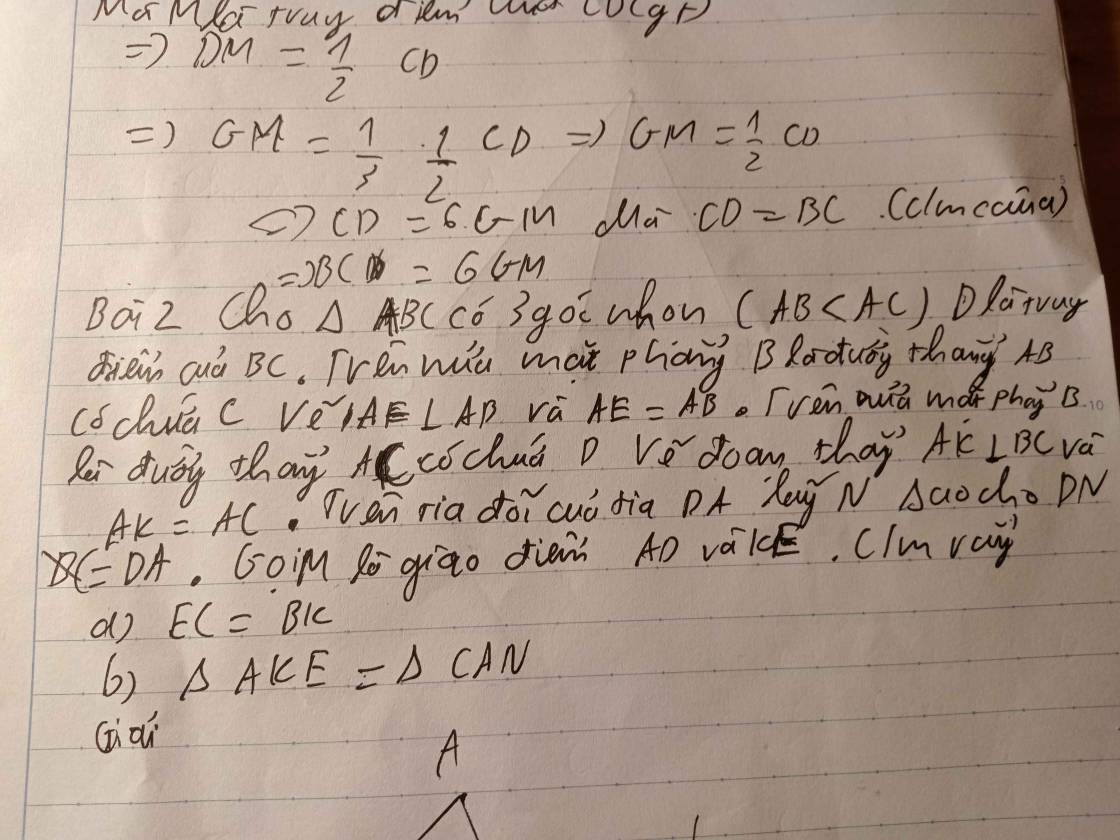
A B C E F D M N
a) Xét \(\bigtriangleup BCE \) và \(\bigtriangleup CBD\) có:
\(EC=BD\left(gt\right)\)
\(\widehat{ECB}=\widehat{CBD}\)(2 góc sole trong do BD//CE)
\(BC-chung\)
\(\implies \bigtriangleup BCE=\bigtriangleup CBD(c.g.c)\)
b) Có: \(\bigtriangleup BCE=\bigtriangleup CBD(cmt)\)
\(\implies EB=CD\)(1)
Có: AB=CD(gt)
\(\Rightarrow\frac{1}{2}AB=\frac{1}{2}CD\Rightarrow EB=CF\)(2)
Từ (1) và (2) \(\implies CD=CF\)
Có: AB=CD(gt)
\(\implies \bigtriangleup ABC\) cân tại A
\(\Rightarrow\widehat{ABC}=\widehat{ACB}\)(2 góc ở đáy)
Xét \(\bigtriangleup ECB\) và \(\bigtriangleup FBC\) có:
\(EB=FC(cmt)\)
\(\widehat{EBC}=\widehat{FCB}\left(cmt\right)\)
\(BC-chung\)
\(\implies \bigtriangleup ECB=\bigtriangleup FBC(c.g.c)\)
\(\implies BF=CE\)(2 cạnh tương ứng)
c) Có: \(\bigtriangleup BCE= \bigtriangleup CBD\)
\(\Rightarrow\widehat{EBC}=\widehat{DCB}\)
Gọi FD giao BC tại N
Xét \(\Delta FCN\) và \(\Delta DCN\) có;
\(CF=CD\)(câu b)
\(\widehat{FCN}=\widehat{DCN}\left(cmt\right)\)
\(CN-chung\)
\(\Rightarrow\Delta FCN=\Delta DCN\left(c.g.c\right)\)
\(\Rightarrow\widehat{CNF}=\widehat{CND}\)(2 góc tương ứng)
Mà \(\widehat{CNF}+\widehat{CND}=180^o\)(2 góc kề bù)
\(\Rightarrow\widehat{CNF}=\widehat{CND}=90^o\Rightarrow FD\perp BC\)
d) Xét \(\Delta EMC\) và \(\Delta DMB\) có:
\(EC=BD\left(gt\right)\)
\(\widehat{ECM}=\widehat{MBD}\)
\(MB=MC\)(vì M-trung điểm BC)
\(\Rightarrow\Delta EMC=\Delta DMB\left(c.g.c\right)\)
\(\Rightarrow\widehat{EMC}=\widehat{DMB}\)(2 góc tương ứng)
Mà \(\widehat{BME}+\widehat{EMC}=180^o\)(2 góc kề bù)
\(\Rightarrow\widehat{BME}+\widehat{DMB}=180^o\)
\(\Rightarrow EM\equiv MD\)
\(\implies E;M;D\) thẳng hàng
_Học tốt_
d) Ta có EC // BD và EC = BD ( tam giác BCE = tam giác CBD )
=> tứ giác BECD là hình bình hành
=> ED giao BC tại trung điểm mỗi đường
Mà M là trung điểm của BC nên M là trung điểm của ED
=> M, E, D thẳng hàng ( đpcm )