k mìnhna
pls
giải
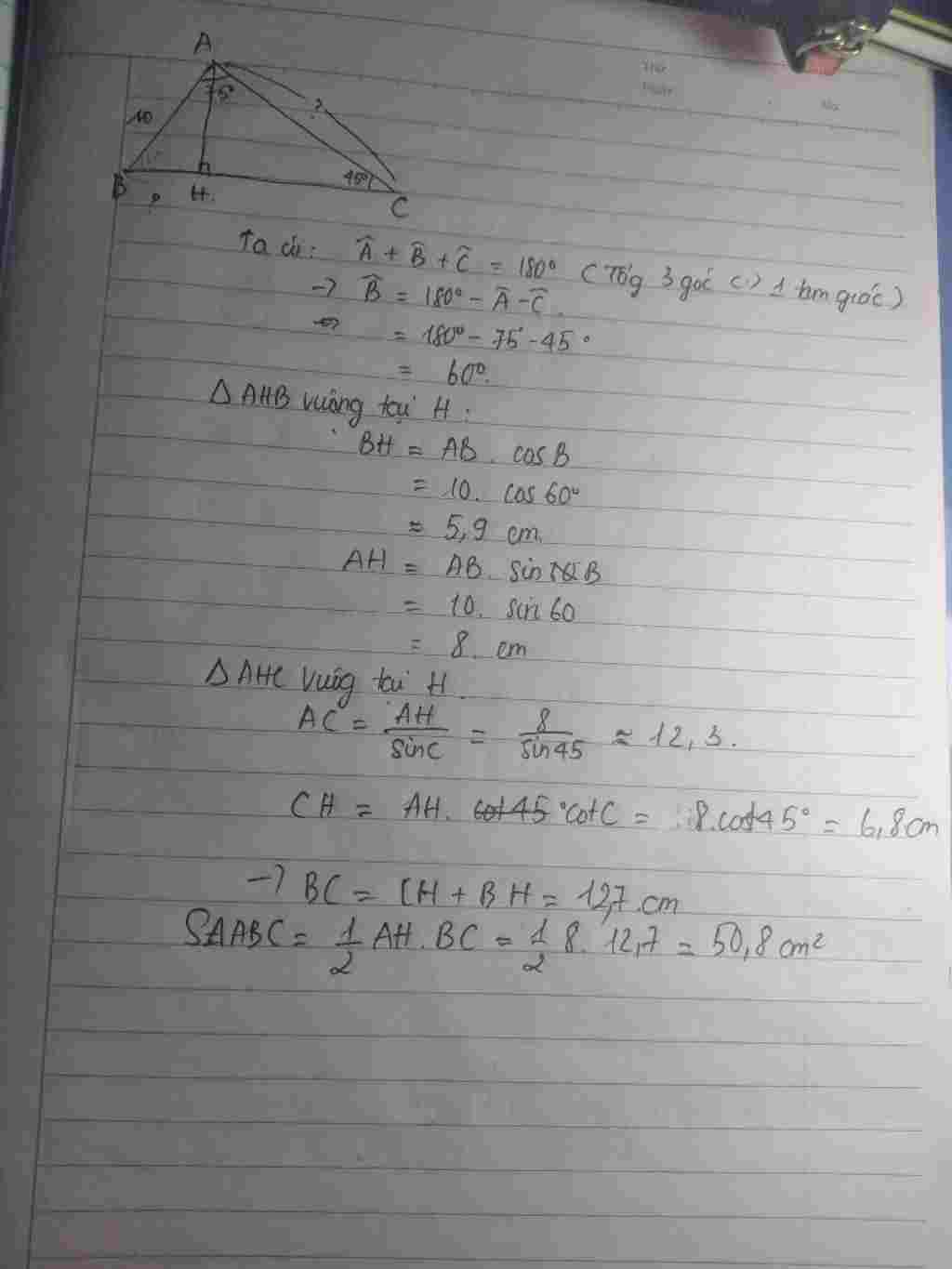
a, Kẻ AH vuông BC .Tính BH,AC v...">
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔABC vuông tại A có \(\widehat{ACB}=45^0\)(gt)
nên ΔABC vuông cân tại A(Định lí tam giác vuông cân)
Suy ra: AB=AC
mà AB=10cm(gt)
nên AC=10cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{AH^2}=\dfrac{1}{10^2}+\dfrac{1}{10^2}=\dfrac{2}{100}=\dfrac{1}{50}\)
\(\Leftrightarrow AH^2=50\)
hay \(AH=5\sqrt{2}\left(cm\right)\)
Xét ΔABH vuông tại H có \(\widehat{B}=45^0\)(ΔABC vuông cân tại A)
nên ΔABH vuông cân tại H
Suy ra: BH=AH
mà \(AH=5\sqrt{2}\left(cm\right)\)(cmt)
nên \(BH=5\sqrt{2}\left(cm\right)\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{10\cdot10}{2}=50\left(cm^2\right)\)
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABH vuông tại H có HE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot AB=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔACH vuông tại H có HF là đường cao ứng với cạnh huyền AC, ta được:
\(AF\cdot AC=AH^2\)(2)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)

Hình bạn tự vẽ nha, thanks ![]()
a)Trong tam giác ABC vuông tại A, có:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+9^2}=\sqrt{117}=3\sqrt{13}\)
\(\tan B=\frac{AC}{AB}=\frac{9}{6}=\frac{3}{2}\Rightarrow\widehat{B}=56^019'\)
\(\Rightarrow\widehat{C}=90^o-\widehat{B}=90^o-56^o19'=34^o41'\)
b)Ta có: AEHF là hình chữ nhật vì \(\widehat{EAF}=\widehat{AEH}=\widehat{AFH}=90^o\)
\(\Rightarrow EF=AH\)
Lại có:\(AH.BC=AB.AC\Rightarrow AH=\frac{AB.AC}{BC}=\frac{6.9}{3\sqrt{13}}=\frac{18\sqrt{13}}{13}\)
Do đó:\(EF=AH=\frac{18\sqrt{13}}{13}\)
c)Ta có: \(\left\{{}\begin{matrix}AE.AB=AH^2\\AF.AC=AH^2\end{matrix}\right.\Rightarrow AE.AB=AF.AC\)
d)Ta có:\(\left\{{}\begin{matrix}\widehat{MEH}+\widehat{HEF}=90^o\\\widehat{MHE}+\widehat{EHA}=90^o\\\widehat{HEF}=\widehat{EHA}\end{matrix}\right.\)\(\Rightarrow\widehat{MEH}=\widehat{MHE}\)
\(\Rightarrow\Delta EHM\) cân tại M
\(\Rightarrow EM=MH\)(1)
Lại có:\(\widehat{BEM}+\widehat{MEF}+\widehat{AEF}=180^o\)
\(\Rightarrow\widehat{BEM}+\widehat{AEF}=180^o-\widehat{MEF}=180^o-90^o=90^o\)
Ta cũng có:\(\widehat{B}+\widehat{C}=90^o\)
Mà \(\widehat{C}=\widehat{HAE}\)(cùng phụ với góc HAC)\(=\widehat{AEF}\)
Do đó:\(\widehat{BEM}=\widehat{B}\)
\(\Rightarrow\Delta BEM\) cân tại M
\(\Rightarrow BM=ME\)(2)
Từ (1) và (2) ta suy ra \(BM=HM\left(=EM\right)\)
Vậy M là trung điểm của BH
Tương tự với N nha :DD
e)\(EM=\frac{1}{2}BH=\frac{1}{2}.\frac{AB^2}{BC}=\frac{1}{2}.\frac{6^2}{3\sqrt{13}}=\frac{6\sqrt{13}}{13}\)
\(FN=\frac{1}{2}HC=\frac{1}{2}.\frac{AC^2}{BC}=\frac{1}{2}.\frac{9^2}{3\sqrt{13}}=\frac{27\sqrt{13}}{26}\)
f)Vì EM//NF(cùng vuông góc với EF)
nên EFNM là hình thang
\(\Rightarrow S_{EFNM}=\frac{1}{2}\left(EM+FN\right).EF=\frac{1}{2}\left(\frac{6\sqrt{13}}{13}+\frac{27\sqrt{13}}{26}\right).\frac{18\sqrt{13}}{13}=13,5\left(đv^2\right)\)
*Nhớ ghi đơn vị là cm hay m gì đó nha, không có đơn vị thấy thiếu thốn cái gì ấy :DD
*Đoạn thẳng có độ dài xấu mà diện tích lại đẹp, không thể tin nổi :DD
*Đang làm đề nên làm hơi chậm :), có gì sai nhớ nhắc mình nha :DD
Bạn tự vẽ hình nha =="
AC = AH + HC = 6 + 4 = 10 (cm)
mà AC = AB (tam giác ABC cân tại A)
=> AB = 10 (cm)
Tam giác HAB vuông tại H có:
AB2 = AH2 + BH2 (định lý Pytago)
102 = 62 + BH2
BH2 = 102 - 62
BH2 = 100 - 36
BH2 = 64
BH = 8 (cm)
Tam giác HBC vuông tại H có:
BC2 = BH2 + CH2
BC2 = 82 + 42
BC2 = 64 + 16
BC2 = 80
BC = √80(cm)80(cm)
Chúc bạn học tốt ^^
Bạn tự vẽ hình nha. Cũng đơn giản lắm....
Xét hai tam giác vuông AHB và BHC có :
AH = HC (= 6cm)
HB là cạnh chung
Do đó : ΔAHB=ΔCHBΔAHB=ΔCHB(cạnh - góc - cạnh)
=> BC = AB ( hai cạnh tương ứng)
Mà AB = AC ( định nghĩa tam giác cân)
=> BC = AB = AH+CH= 12cm