Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
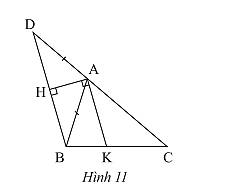
a) Vì \(\left\{ \begin{array}{l}AK \bot HA\\BD \bot HA\end{array} \right. \Rightarrow AK//BD\) (từ vuông góc đến song song)
Xét tam giác \(BCD\) có \(AK//BD\), theo định lí Thales ta có:
\(\frac{{KC}}{{KB}} = \frac{{AC}}{{AD}}\).
Mà \(AD = AB\) (gt), nên \(\frac{{KC}}{{KB}} = \frac{{AC}}{{AB}}\).
Xét tam giác \(ABC\) ta có:
\(\frac{{KC}}{{KB}} = \frac{{AC}}{{AB}} \Rightarrow AK\) là đường phân giác của góc \(A\) trong tam giác \(ABC\).
b) Vẽ đường phân giác của một góc trong tam giác bằng thước kẻ và eke.
Giả sử ta vẽ đường phân giác góc \(A\) của tam giác \(ABC\).
Bước 1: Trên tia đối của tia \(AC\) lầy điểm \(D\) sao cho \(AD = AC\);
Bước 2: Vẽ \(AH\) vuông góc với \(BD\);
Bước 3: Vẽ \(AK\) vuông góc với \(AH\) tại \(A\).
Bước 4: Khi đó, \(AK\) là đường phân giác góc \(A\) trong tam giác \(ABC\).
a: AK//BD(cùng vuông góc với AH)
=>góc CAK=góc D; góc BAK=góc ABD
mà góc D=góc ABD
nên góc CAK=góc BAK
=>AK là phân giác của góc BAC
b: 
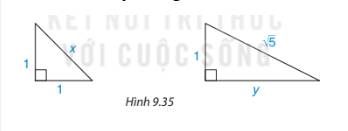
\(x^2=1^2+1^2\left(pythagore\right)\\ \Rightarrow x=\sqrt{2}\\ \sqrt{5}^2=1^2+y^2\left(pythagore\right)\\ \Rightarrow y=\sqrt{4}=2\)
a) \(x^2=1^2+1^2=2\Rightarrow x=\sqrt[]{2}\)
b) \(\left(\sqrt[]{5}\right)^2=y^2+1^2\Rightarrow y^2=5-1=4\Rightarrow y=2\)
trong công cụ 
để kiểm tra trung điểm AC và BD có trùng nhau không.
a) Dùng 
trong công cụ 
để kiểm tra trung điểm AC và BD, ta thấy trung điểm AC và BD trùng nhau.
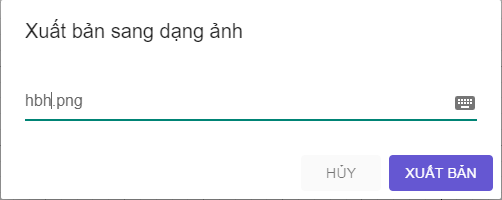
b) Lưu hình vẽ ở HĐ2 thành tệp hbh.png.
Vào Hồ sơ → Chọn Xuất bản → Chọn PNG image (.png).
Ta đổi tên tệp thành hbh (như hình vẽ), sau đó chọn xuất bản.
Bước 1. Vẽ đoạn thẳng AB và có độ dài 4 cm tương tự như Bước 1 của HĐ1.
Bước 2. Vẽ điểm C sao cho BC = 4 cm.
Chọn công cụ 
→ Chọn 
→ Nháy chuột vào điểm B, nhập bán kính bằng 4.
Chọn công cụ 
→ Chọn 
→ Chọn điểm C bất kỳ nằm trên đường tròn tâm B.
Chọn công cụ 
→ Chọn 
→ Nháy chuột vào điểm C, nhập bán kính bằng 4.
Chọn công cụ 
→ Chọn 
→ Lần lượt nháy chuột đường tròn tâm A và đường tròn C.
Chọn công cụ 
để nối B với C, C với D, D với A.
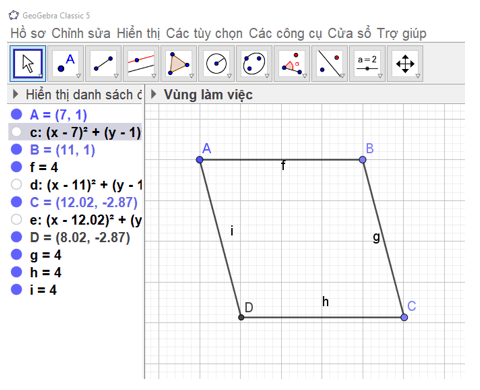
Bước 3. Ẩn đường tròn và thu được hình thoi ABCD.
Tỉ số:
\(\frac{{DE}}{{AC}} = \frac{6}{8} = \frac{3}{4};\frac{{EF}}{{BC}} = \frac{{15}}{{20}} = \frac{3}{4}\).
Xét tam giác\(DEF\) và tam giác\(ABC\) có:
\(\frac{{DE}}{{AC}} = \frac{{EF}}{{BC}} = \frac{3}{4}\) (chứng minh trên)
Do đó, \(\Delta DEF\backsim\Delta ABC\).
Tỉ số:
\(\frac{{DE}}{{MN}} = \frac{6}{3} = 2;\frac{{EF}}{{NP}} = \frac{{15}}{6} = \frac{5}{2}\).
Vì \(\frac{{DE}}{{MN}} \ne \frac{{EF}}{{NP}}\) nên hai tam giác \(DEF\) và \(MNP\) không đồng dạng với nhau.
Tỉ số:
\(\frac{{DE}}{{RS}} = \frac{6}{4} = \frac{3}{2};\frac{{EF}}{{ST}} = \frac{{15}}{{12}} = \frac{5}{4}\).
Vì \(\frac{{DE}}{{RS}} \ne \frac{{EF}}{{ST}}\) nên hai tam giác \(DEF\) và \(SRT\) không đồng dạng với nhau.
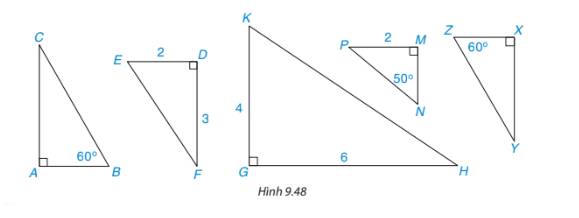
Cặp tam giác vuông ở hình d. Vì cạnh huyền và một cạnh góc vuông của tam giác này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia
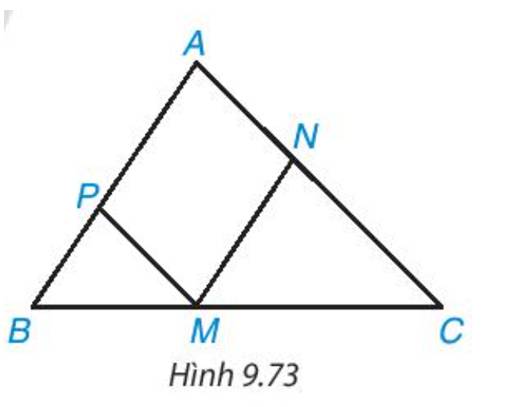
- ΔCNM ~ ΔCAB (vì MN // AB) (1)
- ΔMPB ~ ΔCAB (vì MP // AC) (2)
- Từ (1) và (2) => ΔCNM ~ ΔMPB
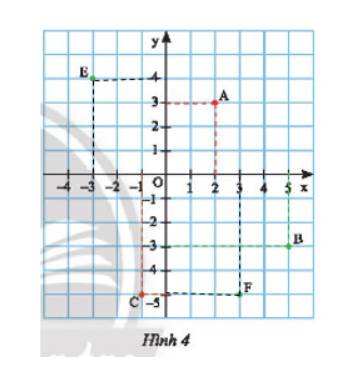
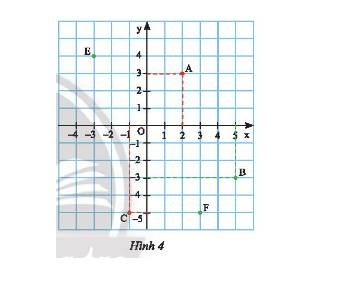
Điểm \(O\) là gốc tọa độ nên \(O\left( {0;0} \right)\)
Từ điểm \(E\) ta vẽ vuông góc với \(Ox;Oy\) cắt \(Ox\) tại – 3 và cắt \(Oy\) tại 4 nên \(E\left( { - 3;4} \right)\).
Từ điểm \(F\) ta vẽ vuông góc với \(Ox;Oy\) cắt \(Ox\) tại 3 và cắt \(Oy\) tại – 5 nên \(E\left( {3; - 5} \right)\).
+Dùng +trong+công+cụ +để+kiểm+tra+trung+điểm+AC+và+BD+có+trùng+nhau+không.b)+Lưu+hình+vẽ+ở+HĐ2+thành+tệp+hbh.png.c)+Tương+tự,+hãy+vẽ+một+hình+thoi+ABCD+có+cạnh+4+cm.){kind=link}
Các cặp tam giác vuông đồng dạng:
\(\begin{array}{l}\Delta ABC \backsim \Delta X{\rm{Z}}Y(\widehat A = \widehat X;\widehat B = \widehat Z)\\\Delta E{\rm{D}}F \backsim \Delta KGH\left( {\frac{{E{\rm{D}}}}{{KG}} = \frac{{DF}}{{GF}};\widehat {E{\rm{D}}F} = \widehat {KGH}} \right)\end{array}\)
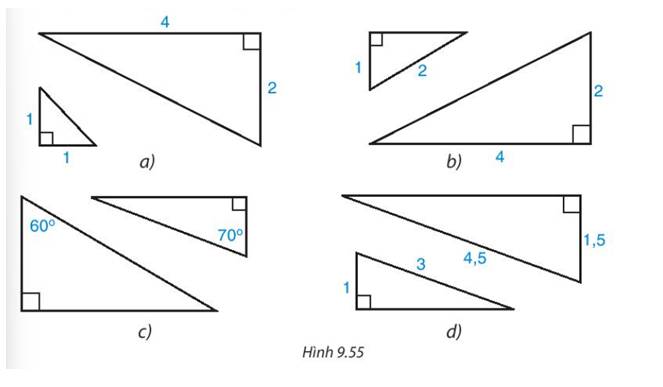
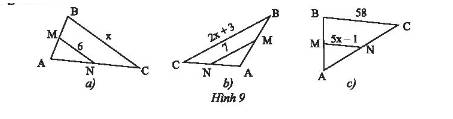
- Hình a:
Vì \(MN\) là đường trung bình của tam giác \(ABC\) nên theo tính chất đường trung bình ta có:
\(\left\{ \begin{array}{l}MN//BC\\MN = \frac{1}{2}BC\end{array} \right. \Rightarrow MN = \frac{1}{2}x \Leftrightarrow 6 = \frac{1}{2}x \Leftrightarrow x = 6:\frac{1}{2} = 12\)
- Hình b:
Vì \(MN\) là đường trung bình của tam giác \(ABC\) nên theo tính chất đường trung bình ta có:
\(\left\{ \begin{array}{l}MN//BC\\MN = \frac{1}{2}BC\end{array} \right. \Rightarrow MN = \frac{1}{2}\left( {x + 3} \right) \Leftrightarrow 7 = \frac{1}{2}\left( {x + 3} \right) \Leftrightarrow \left( {x + 3} \right) = 7:\frac{1}{2} = 14\)
\( \Rightarrow x = 14 - 3 \Leftrightarrow x = 11\).
- Hình c
Vì \(MN\) là đường trung bình của tam giác \(ABC\) nên theo tính chất đường trung bình ta có:
\[\left\{ \begin{array}{l}MN//BC\\MN = \frac{1}{2}BC\end{array} \right. \Rightarrow MN = \frac{1}{2}.58 \Leftrightarrow \left( {5x - 1} \right) = \frac{1}{2}.58\]
\[ \Leftrightarrow \left( {5x - 1} \right) = 29 \Leftrightarrow 5x = 30 \Leftrightarrow x = 30:5 \Leftrightarrow x = 6\].
a: MN là đường trung bình
=>MN=BC/2
=>x=6*2=12
b: MN là đường trung bình
=>2x+3=2*7=14
=>2x=11
=>x=11/2
c: MN là đường trung bình
=>5x-1=58/2=29
=>5x=30
=>x=6